题目内容
已知函数f（x）的定义域是[0，2]，则函数y=f（x+1）的定义域是 ．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据题意可知0≤x+1≤2，求出x的范围并用区间表示，即可所求函数的定义域．
解答：
解：∵函数f（x）的定义域为[0，2]，
∴0≤x+1≤2，解得-1≤x≤1，
∴所求函数y=f（x+1）的定义域是[-1，1]
故答案为：[-1，1]
∴0≤x+1≤2，解得-1≤x≤1，
∴所求函数y=f（x+1）的定义域是[-1，1]
故答案为：[-1，1]
点评：本题主要考查了抽象函数的定义域的求法，以及不等式的解法，属于基础题．
练习册系列答案
相关题目
若0＜x＜
，0＜y＜
，且sinx=xcosy，则（ ）
| π |
| 2 |
| π |
| 2 |
A、y＜
| ||||
B、
| ||||
C、
| ||||
| D、x＜y |
如图所示正方体AC1，下面结论错误的是（ ）
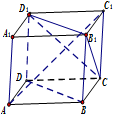
| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AD与CB1角为60° |
下列各组函数f（x）与g（x）的图象相同的是（ ）
A、f（x）=x，g（x）=（
| |||||
| B、f（x）=x2，g（x）=（x+1）2 | |||||
C、f（x）=|x|，g（c）=
| |||||
| D、f（x）=1，g（x）=x0 |
数列-
，
，-
，
，…的一个通项公式是（ ）
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
| 25 |
| 9 |
A、an=（-1）n
| ||
B、an=（-1）n
| ||
C、an=（-1）n
| ||
D、an=（-1）n
|
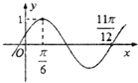函数f（x）=Asin（ωx+∅）（A＞0，ω＞0，|∅|＜| π |
| 2 |
| 1 |
| 2 |
A、y=sin（4x+
| ||
B、y=sin（4x+
| ||
C、y=sin（x+
| ||
D、y=sin（x+
|
如图，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=1，AB=2，M是PB的中点．