题目内容
设函数f(x)=x
-
对于任意x∈[-1,1],都有f(x)≤0成立,则实数a的范围 .
| a-x2 |
| 1 |
| 2 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:问题可化为4ax2≤4x4+1恒成立,当x=0时,上式显然成立,当x∈[-1,0)∪(0,1]时,4ax2≤4x4+1可化为a≤
,只需求
在x∈[-1,0)∪(0,1]时的最小值即可,由基本不等式可得.
| 4x4+1 |
| 4x2 |
| 4x4+1 |
| 4x2 |
解答:
解:由f(x)≤0可得x2(a-x2)≤
,即4ax2≤4x4+1,
当x=0时,上式显然成立,
当x∈[-1,0)∪(0,1]时,
4ax2≤4x4+1可化为a≤
,
故只需求
在x∈[-1,0)∪(0,1]时的最小值即可,
由基本不等式可得
=x2+
≥2
=1,
当且仅当x2=
即x=±
时取等号,
∴
在x∈[-1,0)∪(0,1]时的最小值为1,
故a≤1
故答案为:a≤1
| 1 |
| 4 |
当x=0时,上式显然成立,
当x∈[-1,0)∪(0,1]时,
4ax2≤4x4+1可化为a≤
| 4x4+1 |
| 4x2 |
故只需求
| 4x4+1 |
| 4x2 |
由基本不等式可得
| 4x4+1 |
| 4x2 |
| 1 |
| 4x2 |
x2•
|
当且仅当x2=
| 1 |
| 4x2 |
| ||
| 2 |
∴
| 4x4+1 |
| 4x2 |
故a≤1
故答案为:a≤1
点评:本题考查不等式恒成立问题,转化为基本不等式求最值是解决问题的关键,属中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
如图所示正方体AC1,下面结论错误的是( )
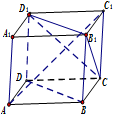

| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AD与CB1角为60° |
数列-
,
,-
,
,…的一个通项公式是( )
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
| 25 |
| 9 |
A、an=(-1)n
| ||
B、an=(-1)n
| ||
C、an=(-1)n
| ||
D、an=(-1)n
|
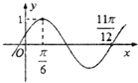 函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<
函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<| π |
| 2 |
| 1 |
| 2 |
A、y=sin(4x+
| ||
B、y=sin(4x+
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|
已知等比数列{an}中,各项都是正数,且a2,
a4,2a3成等差数列,则
=( )
| 1 |
| 2 |
| a7+a8 |
| a5+a6 |
A、1+
| ||
B、1-
| ||
C、3+2
| ||
D、3-2
|