题目内容
9.已知f(x)是定义在R上的单调函数,f(1)=2且对于任意x,y∈R,总有f(x+y)=f(x)+f(y),(1)求f(0)、f(3)的值;
(2)若f(4x-a)+f(6+2x+1)>6对任意x恒成立,求实数a的取值范围.
分析 (1)令x=y=0,可得f(0)=0;令x=y=1,再令x=1,y=2,即可得到f(3)=6;
(2)由(1)的结论可得f(x)为R上的递增函数,令y=-x,可得f(-x)=-f(x),由题意可得4x-a>-3-2x+1,即a-3<4x+2x+1,求得右边函数的值域,即可得到a的范围.
解答 解:(1)令x=y=0,则f(0)=2f(0),解得f(0)=0;
令x=y=1,则f(2)=2f(1)=4;
再令x=1,y=2,则f(3)=f(1)+f(2)=2+4=6;
(2)由f(x)是定义在R上的单调函数,且f(0)<f(1),f(2)<f(3),
则f(x)在R上为递增函数,
由y=-x,可得f(0)=f(x)+f(-x)=0,
即为f(-x)=-f(x),
f(4x-a)+f(6+2x+1)>6对任意x恒成立,
即有f(4x-a)>6-f(6+2x+1)=f(3)+f(-6-2x+1)=f(-3-2x+1),
即为4x-a>-3-2x+1,即a-3<4x+2x+1,
由4x+2x+1=(2x+1)2-1>0,
可得a-3≤0,解得a≤3.
故实数a的取值范围是(-∞,3].
点评 本题考查函数的单调性和奇偶性的判断和运用:解不等式,同时考查赋值法的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.a、b表示两条直线,α、β、γ表示三个平面,下列命题中错误的是( )
| A. | a?α,b?α,且a∥β,b∥β,则α∥β | |
| B. | a、b是异面直线,则存在唯一的平面与a、b等距 | |
| C. | a⊥α,b?β,a⊥b,则α∥β | |
| D. | α⊥γ,γ∥β,a⊥α,b⊥β,则a⊥b |
17.小明同学每天下午4:00到5:00之间放学到家学习,小刚同学每天下午4:30到5:30之间到达小明家给他辅导功课,则小刚到小明家时就能见到小明的概率是( )
| A. | 1 | B. | 0.875 | C. | 0.65 | D. | 0.5 |
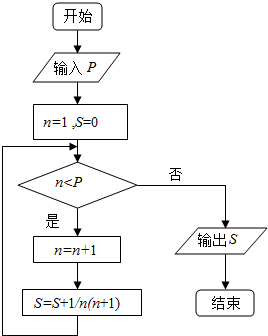 执行如图的程序框图,若p=7,则输出的s=$\frac{3}{8}$.
执行如图的程序框图,若p=7,则输出的s=$\frac{3}{8}$.