题目内容
17．小明同学每天下午4：00到5：00之间放学到家学习，小刚同学每天下午4：30到5：30之间到达小明家给他辅导功课，则小刚到小明家时就能见到小明的概率是（ ）| A． | 1 | B． | 0.875 | C． | 0.65 | D． | 0.5 |
分析 设小明x时刻到家，则4＜x＜5，小刚y时刻到小明家，则4.5＜y＜5.5，满足题意需y≥x，作图由几何概型的概率公式可得．
解答 
解：设小明x时刻到家，则4＜x＜5，小刚y时刻到小明家，则4.5＜y＜5.5，
两人若要相会，需y≥x，即小刚在小明到家之后到达．
如图所示，由几何概型求得P=0.875
故选：B．
点评 本题考查几何概型的会面问题，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
8．
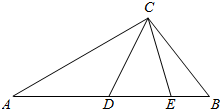如图△ABC中，C=$\frac{π}{2}$，AC=$\sqrt{3}$，BC=1，D，E为线段AB的点，∠ACD=$\frac{π}{4}$，∠DCE=$\frac{π}{6}$，则△DCE的面积为（ ）
如图△ABC中，C=$\frac{π}{2}$，AC=$\sqrt{3}$，BC=1，D，E为线段AB的点，∠ACD=$\frac{π}{4}$，∠DCE=$\frac{π}{6}$，则△DCE的面积为（ ）| A． | $\frac{6-3\sqrt{3}}{4}$ | B． | $\frac{9-3\sqrt{3}}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{\sqrt{3}}{8}$ |
12．函数f（x）=sinx+$\frac{1}{lnx}$的定义域是（ ）
| A． | （0，+∞） | B． | （e，+∞） | C． | （0，1）∪（1，+∞） | D． | （1，e）∪（e，+∞） |
在某中学举行的环保知识竞赛中，随机抽取x名参赛同学的成绩（得分的整数）进行整理后分成五组，绘制出如图所示的频率分布直方图，已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30，0.15，0.10，0.05，第二小组的频数为40．