题目内容
18．设函数f（x）=x-$\frac{1}{x}$-alnx．（1）若曲线y=f（x）在点（1，f（1））处的切线与圆x2+y2=$\frac{1}{2}$，求a的值；
（2）当a∈[0，2]时，函数g（x）=x-lnx-$\frac{1}{e}$，若在[1，e]上至少存在一根x0，使得f（x0）≥g（x0），求实数a的取值范围．
分析 （1）求出导数，求得切线的斜率和切点，求出切线的方程，由直线和圆相切的条件，即可得到a的值；
（2）求出g（x）的导数，判断单调性，求得在[1，e]上的最小值，求出f（x）的导数，判断单调性，可得最大值，若在[1，e]上存在实数x，使得f（x）＞g（x），即为f（x）max≥g（x）min，解不等式即可得到a的范围．
解答 解：（1）函数f（x）=x-$\frac{1}{x}$-alnx的导数为f′（x）=1+$\frac{1}{{x}^{2}}$-$\frac{a}{x}$，
在点（1，f（1））处的切线斜率为2-a，切点为（1，0），
在点（1，f（1））处的切线方程为y=（2-a）（x-1），
切线与圆x2+y2=$\frac{1}{2}$相切，可得$\frac{|2-a|}{\sqrt{1+（2-a）^{2}}}$=$\frac{\sqrt{2}}{2}$，
解得a=1或3；
（2）∵g（x）=x-lnx-$\frac{1}{e}$的导数为g′（x）=1-$\frac{1}{x}$=$\frac{x-1}{x}$≥0，
则g（x）在[1，e]上是增函数，
∴x=1时，g（x）min=1-$\frac{1}{e}$；
又f（x）=x-$\frac{1}{x}$-alnx的导数为f′（x）=1+$\frac{1}{{x}^{2}}$-$\frac{a}{x}$=$\frac{{x}^{2}-ax+1}{{x}^{2}}$，
由a∈[0，2]，则x2-ax+1的判别式a2-4≤0，即有f′（x）≥0恒成立，
即f（x）在[1，e]递增，x=e处取得最大值，且为e-$\frac{1}{e}$-a，
由在[1，e]上至少存在一根x0，使得f（x0）≥g（x0），
即有f（x）max≥g（x）min，即为e-$\frac{1}{e}$-a≥1-$\frac{1}{e}$，
解得0≤a≤e-1，
则a的取值范围是[0，e-1]．
点评 本题主要考查对数函数的导数，函数单调性的判定，函数最值，函数、方程与不等式等基础知识，考查学生的运算求解能力、推理论证能力及分析与解决问题的能力，属于中档题．
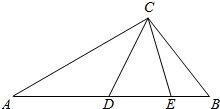如图△ABC中，C=$\frac{π}{2}$，AC=$\sqrt{3}$，BC=1，D，E为线段AB的点，∠ACD=$\frac{π}{4}$，∠DCE=$\frac{π}{6}$，则△DCE的面积为（ ）| A． | $\frac{6-3\sqrt{3}}{4}$ | B． | $\frac{9-3\sqrt{3}}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{\sqrt{3}}{8}$ |
| A． | f（$\frac{π}{3}$）＞$\sqrt{2}$f（$\frac{π}{4}$） | B． | f（$\frac{π}{3}$）＞2cos1•f（1） | C． | f（$\frac{π}{4}$）＜2cos1•f（1） | D． | f（$\frac{π}{4}$）＜$\frac{\sqrt{6}}{2}$f（$\frac{π}{6}$） |