题目内容
一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为 .
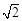 .
.试题解析:因正方体可以在正四面体纸盒内任意转动,所以正方体在正四面体的内切球中,则正方体棱长最大时,正方体的对角线是内切球的直径,如图所示,点O为内切球的圆心,连接PO并延长交底面ABC与点D,点D是底面三角形ABC的的中心,则
 ,则有OD为内切球的的半径,再连接BO,则BO=OP,在
,则有OD为内切球的的半径,再连接BO,则BO=OP,在 中,易知
中,易知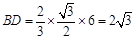 ,
,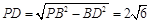 ,在
,在 中,
中,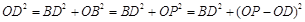 ,代入数据得
,代入数据得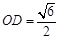 ,令正方体棱长为
,令正方体棱长为 ,则
,则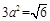 ,
,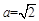 ,即正方体棱长的最大值为
,即正方体棱长的最大值为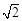 .
.
练习册系列答案
相关题目
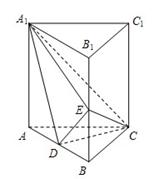
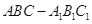 中,
中,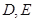 分别是
分别是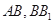 的中点,
的中点,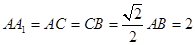 .
.
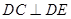 ;
;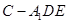 的体积.
的体积.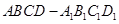 的外接球
的外接球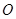 的体积为
的体积为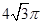 ,则球心
,则球心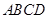 的距离为( )
的距离为( )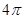 ,底面积为
,底面积为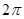 ,则该圆锥的母线长为 .
,则该圆锥的母线长为 . 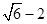
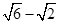
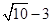
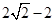
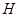 是球
是球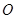 的直径
的直径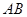 上一点,
上一点,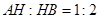 ,
,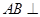 平面
平面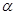 ,
,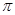 ,则球
,则球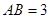 ,
,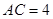 ,则它绕
,则它绕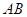 旋转一周得到的旋转体的体积为 .
旋转一周得到的旋转体的体积为 .