题目内容
【题目】如图，设F1，F2是椭圆C：
（a＞b＞0）的左、右焦点，直线y＝kx（k＞0）与椭圆C交于A，B.已知椭圆C的焦距是2，四边形AF1BF2的周长是4
.
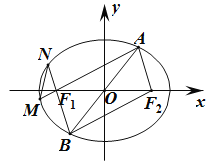
（1）求椭圆C的方程；
（2）直线AF1，BF1分别与椭圆C交于M，N，求△MNF1面积的最大值.
【答案】（1）
＝1；（2）
【解析】
（1）由题意可得2c＝2，4a＝4
，b2＝a2﹣c2，由此能求出椭圆的方程.
（2）设A（x0，y0），B（﹣x0，﹣y0），则直线AF1：
，直线BF1：
，联立求出
，
，xN＝
，由M，N，E三点共线得kME＝kNE，得t＝﹣
，由此能求出△MNF1面积的最大值.
（1）由题意可得2c＝2，4a＝4，b2＝a2﹣c2，解得：a2＝2，b2＝1，
∴椭圆的方程为：＝1.
（2）设A（x0，y0），（x0＞0，y0＞0），B（﹣x0，﹣y0），
则直线AF1：
，直线BF1：
联立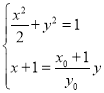
，得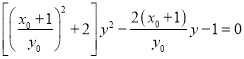
，
又
＝1，代入化简得
＝0，
∴y0yM＝﹣
，∴，∴＝﹣
，
同理得
，xN＝，设直线MN与x轴交于E（t，0），
由M，N，E三点共线得kME＝kNE，得t＝﹣，
∴
＝
＝
＝
≤，当
时，取等号.
∴△MNF1面积的最大值为。
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】某工厂今年前5个月某种产品的产量（单位：万件）的数据如下表：
| 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 4 | 6 | 6 |
（1）若从这5组数据中随机抽出2组，求抽出的2组数据恰好是不相邻两个月的数据的概率；
（2）求出
关于
的线性回归方程
，并估计今年6月份该种产品的产量.
参考公式：
.
