题目内容
【题目】在平面直角坐标系xOy中，直线l过点A（0，5）且与曲线x2+y2＝5（x＞0）相切于点B，则直线l的方程是_____，设E是线段OB中点，长度为
的线段PQ（P在Q的上方）在直线l上滑动，则|OP|+|EQ|的最小值是_____.
【答案】2x﹣y+5＝0或2x+y﹣5＝0 
【解析】
由直线与圆相切求出切线的斜率即可得知切线的方程；作出图象，结合勾股定理表示出|OP|+|EQ|＝
，所以当
时，|OP|+|EQ|取得最小值.
①显然直线l的斜率一定存在，所以设直线l的方程为：y＝kx+5，即kx﹣y+5＝0，
∵直线l与曲线x2+y2＝5（x＞0）相切，∴
，解得：k＝±2，
∴直线l的方程为：2x﹣y+5＝0或2x+y﹣5＝0.
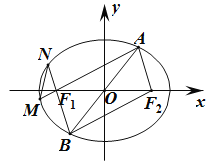
②由①可知，直线l的两条方程关于y轴对称，所以不妨取直线l的方程为2x﹣y+5＝0，
如图所示，由勾股定理得，
，
＝
＝
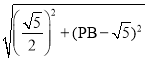，所以|OP|+|EQ|＝，
当时，|OP|+|EQ|取得最小值，为.
故答案为：2x﹣y+5＝0或2x+y﹣5＝0；.
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
