题目内容
(本题满分12分)
设数列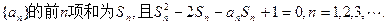
(1)求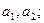
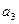 ;
;
(2)求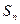 的表达式.
的表达式.
设数列
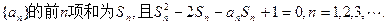
(1)求
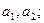
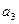 ;
; (2)求
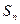 的表达式.
的表达式.解:(1)当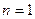 时,由已知得
时,由已知得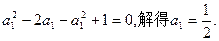
同理,可解得
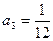 5分
5分
(2)解法一:由题设 当
当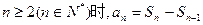
代入上式,得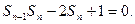 (*) 6分
(*) 6分
由(1)可得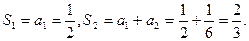 由(*)式可得
由(*)式可得
由此猜想: 8分
8分
证明:①当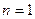 时,结论成立.②假设当
时,结论成立.②假设当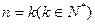 时结论成立,
时结论成立,
即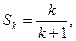 那么,由(*)得
那么,由(*)得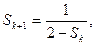
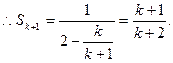
所以当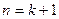 时结论也成立,根据①和②可知,
时结论也成立,根据①和②可知,
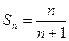 对所有正整数n都成立.因
对所有正整数n都成立.因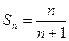 12分
12分
解法二:由题设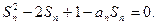 当
当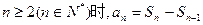
代入上式,得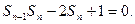
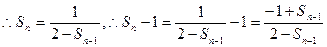
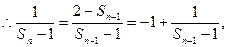
 -1的等差数列,
-1的等差数列,
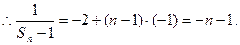
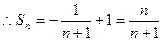
 12分
12分
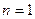 时,由已知得
时,由已知得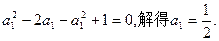
同理,可解得

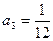 5分
5分(2)解法一:由题设
 当
当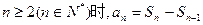
代入上式,得
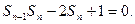 (*) 6分
(*) 6分由(1)可得
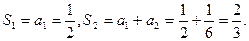 由(*)式可得
由(*)式可得
由此猜想:
 8分
8分证明:①当
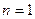 时,结论成立.②假设当
时,结论成立.②假设当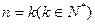 时结论成立,
时结论成立,即
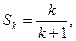 那么,由(*)得
那么,由(*)得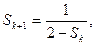
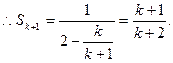
所以当
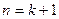 时结论也成立,根据①和②可知,
时结论也成立,根据①和②可知,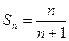 对所有正整数n都成立.因
对所有正整数n都成立.因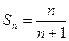 12分
12分解法二:由题设
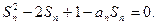 当
当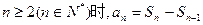
代入上式,得
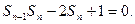
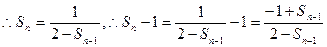
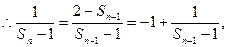
 -1的等差数列,
-1的等差数列,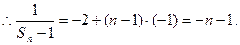
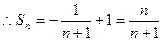
 12分
12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
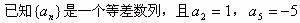

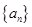 是等差数列且
是等差数列且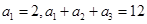 。(1)求数列
。(1)求数列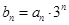 ,求数列
,求数列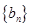 的前
的前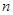 项和
项和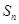 。
。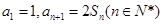 。(1)求数列
。(1)求数列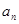 (2)求数列
(2)求数列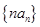 前
前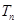 。
。 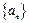 是公差为
是公差为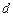 的等差数列,其前
的等差数列,其前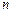 项和为
项和为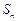 .
.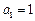 ,
,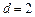 ,
,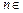
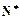 时,
时,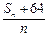 的最小值;
的最小值;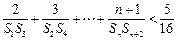 ;
;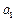 ,使得对任意正整数
,使得对任意正整数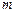 的不等式
的不等式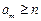 的最小正整数解为
的最小正整数解为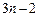 ?若存在,则求
?若存在,则求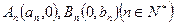 ,其中数列
,其中数列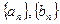 都是递增数列。
都是递增数列。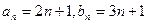 ,判断直线
,判断直线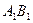 与
与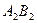 是否平行;
是否平行;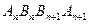 的面积为
的面积为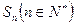 .
.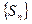 也是等差数列;
也是等差数列;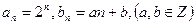 ,
,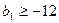 ,记直线
,记直线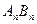 的斜率为
的斜率为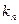 ,数列
,数列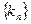 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列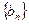 的个数。
的个数。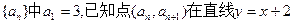 上,
上,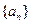 的通项公式;
的通项公式;
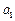 和正数
和正数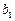 ,且对任意的正整数n,当
,且对任意的正整数n,当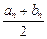 ≥0时, 有[
≥0时, 有[ ,
, 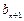 ]=
]=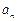 ,
, 
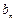 ].
].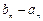 }是等比数列;
}是等比数列; ,求证
,求证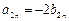
 ;
; ,使得数列
,使得数列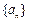 为常数数列?请说明理由
为常数数列?请说明理由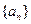 的前20项的和为100,那么
的前20项的和为100,那么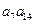 的最大值为( )
的最大值为( )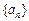 满足
满足 ,且
,且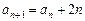 ,
,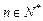 ,那么
,那么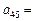 。
。