题目内容
(本小题满分12分已知f(x)是实数集R上的函数,且对任意x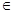 R,f(x)=f(x+1)+f(x-1)恒成立.
R,f(x)=f(x+1)+f(x-1)恒成立.
(Ⅰ)求证:f(x)是周期函数.
(Ⅱ)已知f(-4)=2,求f(2012).
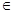 R,f(x)=f(x+1)+f(x-1)恒成立.
R,f(x)=f(x+1)+f(x-1)恒成立.(Ⅰ)求证:f(x)是周期函数.
(Ⅱ)已知f(-4)=2,求f(2012).
(1)证明 ∵f(x)=f(x+1)+f(x-1)∴f(x+1)=f(x)-f(x-1),
则f(x+2)=f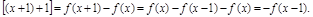
∴f(x+3)=f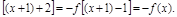 ……………5分
……………5分
f (x+6)=f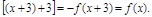
∴f(x)是周期函数且6是它的一个周期. …………………7分
(2)解
f(2 012)=f(335×6+2)=f(2)=f(6+(-4))=f(-4)=2.……12分
则f(x+2)=f
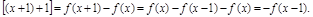
∴f(x+3)=f
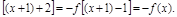 ……………5分
……………5分f (x+6)=f
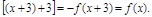
∴f(x)是周期函数且6是它的一个周期. …………………7分
(2)解
f(2 012)=f(335×6+2)=f(2)=f(6+(-4))=f(-4)=2.……12分
略

练习册系列答案
相关题目
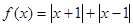 , (2)
, (2)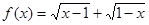 ,(3)
,(3)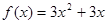 ,(4)
,(4)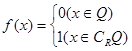 .其中是偶函数的个数为 ( )
.其中是偶函数的个数为 ( )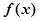 是
是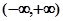 上的偶函数,若对于
上的偶函数,若对于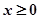 ,都有
,都有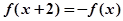 ,且当
,且当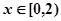 时,
时, ,则
,则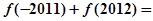 ( )
( )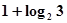
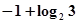
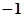
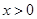 时,
时,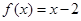 ,那么不等式
,那么不等式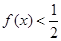 的解集是 ( )
的解集是 ( )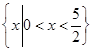
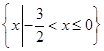
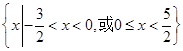
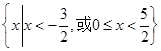
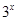 ,则当x<0时,f(x)=_______
,则当x<0时,f(x)=_______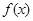 是上的奇函数,
是上的奇函数,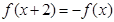 ,当
,当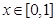 时
时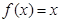 则
则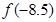 的
的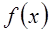 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当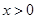 时,f(x)=log2x求
时,f(x)=log2x求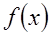 的解析式。
的解析式。