题目内容
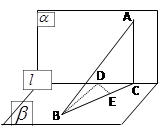
(本题满分12分)已知斜三棱柱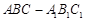 的底面是直角三角形,
的底面是直角三角形,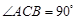 ,侧棱与底面所成角为
,侧棱与底面所成角为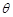 ,点
,点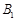 在底面上射影D落在BC上.
在底面上射影D落在BC上.
(Ⅰ)求证: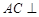 平面
平面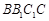 ;
;
(Ⅱ)若点D恰为BC中点,且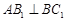 ,求
,求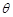 的大小;
的大小;
(III)若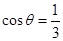 ,且当
,且当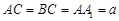 时,求二面角
时,求二面角 的大小.
的大小.

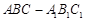 的底面是直角三角形,
的底面是直角三角形,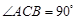 ,侧棱与底面所成角为
,侧棱与底面所成角为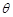 ,点
,点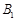 在底面上射影D落在BC上.
在底面上射影D落在BC上.(Ⅰ)求证:
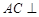 平面
平面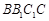 ;
;(Ⅱ)若点D恰为BC中点,且
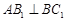 ,求
,求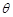 的大小;
的大小;(III)若
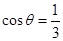 ,且当
,且当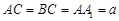 时,求二面角
时,求二面角 的大小.
的大小.
解:(I)∵B1D⊥平面ABC,AC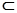 平面ABC,∴
平面ABC,∴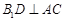
又∵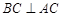 ,
,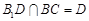 ,∴AC⊥平面
,∴AC⊥平面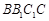
(II)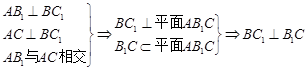
∴四边形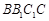 为菱形, 又∵D为BC的中点,
为菱形, 又∵D为BC的中点,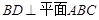
∴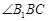 为侧棱和底面所成的角
为侧棱和底面所成的角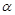 ,∴
,∴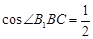
∴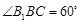 ,即侧棱与底面所成角
,即侧棱与底面所成角 .
.
(III)以C为原点,CA为x轴CB为y轴,过C点且垂直于平面ABC的直线为Z轴,建立空间直角坐标系,
则A(a,0,0),B(0,a,0),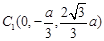 ,平面ABC的法向量
,平面ABC的法向量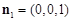 ,设平面ABC1的法向量为
,设平面ABC1的法向量为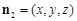 ,
,
由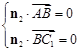 ,即
,即 ,
,
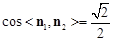 ,
,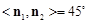
∵二面角 大小是锐二面角,∴二面角
大小是锐二面角,∴二面角 的大小是
的大小是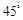 .
.
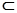 平面ABC,∴
平面ABC,∴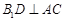
又∵
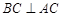 ,
,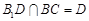 ,∴AC⊥平面
,∴AC⊥平面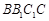
(II)
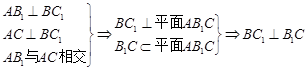
∴四边形
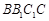 为菱形, 又∵D为BC的中点,
为菱形, 又∵D为BC的中点,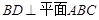
∴
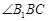 为侧棱和底面所成的角
为侧棱和底面所成的角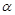 ,∴
,∴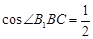
∴
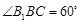 ,即侧棱与底面所成角
,即侧棱与底面所成角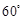 .
.(III)以C为原点,CA为x轴CB为y轴,过C点且垂直于平面ABC的直线为Z轴,建立空间直角坐标系,
则A(a,0,0),B(0,a,0),
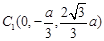 ,平面ABC的法向量
,平面ABC的法向量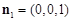 ,设平面ABC1的法向量为
,设平面ABC1的法向量为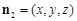 ,
,由
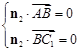 ,即
,即 ,
,
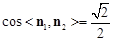 ,
,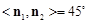
∵二面角
 大小是锐二面角,∴二面角
大小是锐二面角,∴二面角 的大小是
的大小是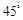 .
. 略

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
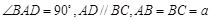 ,
,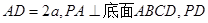 与底面成30°角.
与底面成30°角.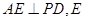 为垂足,求证:
为垂足,求证: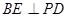 ;
;
 中,
中, 为
为 的中点,
的中点,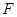 为
为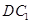 的中点.
的中点.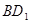 //平面
//平面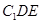 ;(2)求三棱锥
;(2)求三棱锥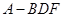 的体积;
的体积;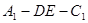 的余弦值。
的余弦值。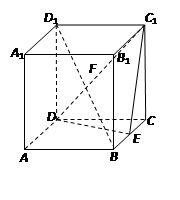
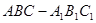 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,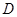 为
为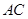 的中点.
的中点.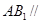 平面
平面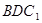 ;
;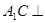 平面
平面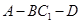 的正切值.
的正切值.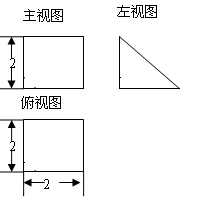
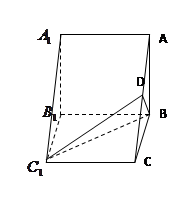
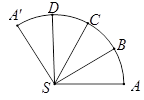
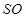 (
(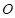 为底面中心)的侧面展开图,
为底面中心)的侧面展开图,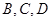 是其侧面展开图中弧
是其侧面展开图中弧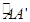 的四等分点,则在圆锥
的四等分点,则在圆锥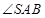 是直线
是直线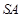 与
与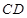 所成的角;
所成的角;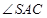 是直线
是直线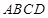 所成的角;
所成的角;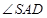 是二面角
是二面角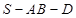 的平面角;
的平面角;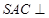 平面
平面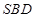
 中,
中, ,
, 为
为 中点,
中点, 为
为 中点,侧面
中点,侧面 为正方形。
为正方形。 平面
平面 ;
; ;
;
 角D1-EC-D的大小为
角D1-EC-D的大小为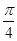 .
.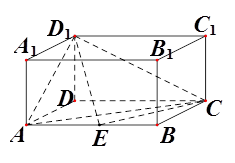
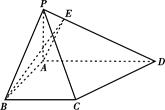
 求平面PAD与平面PBC所成锐二面角的正切值。
求平面PAD与平面PBC所成锐二面角的正切值。
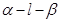 ,点
,点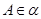 ,
,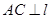 ,
,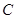 为垂足,
为垂足,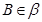 ,
,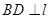 ,
,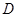 为垂 ( )
为垂 ( ) ,则
,则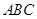 的距离等于
的距离等于