题目内容
【题目】设函数f(x)=|2x+1|+|x﹣a|,a∈R. (Ⅰ)当a=2时,求不等式f(x)<4的解集.
(Ⅱ)当a< ![]() 时,对于x∈(﹣∞,﹣
时,对于x∈(﹣∞,﹣ ![]() ],都有f(x)+x≥3成立,求a的取值范围.
],都有f(x)+x≥3成立,求a的取值范围.
【答案】解:(1)令|2x+1|=0,解得x=﹣ ![]() ,令|x﹣2|=0,解得x=2. 当x≥2时,原不等式化为:2x+1+x﹣2<4,解得x
,令|x﹣2|=0,解得x=2. 当x≥2时,原不等式化为:2x+1+x﹣2<4,解得x ![]() ,此时无解;
,此时无解;
当 ![]() <x<2时,原不等式化为:2x+1+2﹣x<4,解得x<1,可得
<x<2时,原不等式化为:2x+1+2﹣x<4,解得x<1,可得 ![]() <x<1;
<x<1;
当 ![]() 时,原不等式化为:﹣2x﹣1+2﹣x<4,解得x>﹣1,可得﹣1<x≤
时,原不等式化为:﹣2x﹣1+2﹣x<4,解得x>﹣1,可得﹣1<x≤ ![]() .
.
综上可得:原不等式的解集为{x|﹣1<x<1};(2)令g(x)=f(x)+x,当x≤ ![]() 时,g(x)=|x﹣a|﹣x﹣1,由a
时,g(x)=|x﹣a|﹣x﹣1,由a ![]() ,
,
可得g(x)= 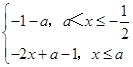 ,对于x∈
,对于x∈ ![]() ,
,
使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈ ![]() ,
,
作出g(x)的图象,可得:[g(x)]min=g(a)=﹣a﹣1,
∴﹣a﹣1≥3,可得a≤﹣4.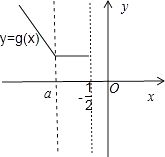
【解析】(1))令|2x+1|=0,解得x=﹣ ![]() ,令|x﹣2|=0,解得x=2.对x分类讨论即可得出.(2)令g(x)=f(x)+x,当x≤
,令|x﹣2|=0,解得x=2.对x分类讨论即可得出.(2)令g(x)=f(x)+x,当x≤ ![]() 时,g(x)=|x﹣a|﹣x﹣1,由a
时,g(x)=|x﹣a|﹣x﹣1,由a ![]() ,可得g(x)=
,可得g(x)= 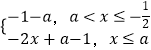 ,对于x∈
,对于x∈ ![]() ,使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈
,使得f(x)+x≥3恒成立.只需[g(x)]min≥3,x∈ ![]() ,利用图象,即可得出.
,利用图象,即可得出.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图:

(1)根据已知条件完成2x2列联表;
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
(2)并判断是否有![]() 的把握认为“阅读达人”跟性别有关?
的把握认为“阅读达人”跟性别有关?
附:参考公式![]()
![]()