题目内容
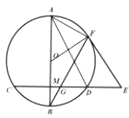
【题目】如图，AB是圆O的直径，弦CD⊥AB于点M，E是CD延长线上一点，AB=10，CD=8，3ED=4OM，EF切圆O于F，BF交CD于G． 
（1）求证：△EFG为等腰三角形；
（2）求线段MG的长．
【答案】
（1）证明：连接AF，OF，则A，F，G，M共圆，∴∠FGE=∠BAF
∵EF⊥OF，
∴∠EFG=∠BAF，
∴∠EFG=∠FGE
∴EF=EG，
∴△EFG为等腰三角形
（2）解：由AB=10，CD=8可得OM=3，
∴ED= 
OM=4EF2=EDEC=48，
∴EF=EG=4 
，
连接AD，则∠BAD=∠BFD，
∴MG=EM﹣EG=8﹣4 ．
【解析】（1）连接AF，OF，则A，F，G，M共圆，∠FGE=∠BAF，证明∠EFG=∠FGE，即可证明：△EFG为等腰三角形；（2）求出EF=EG=4 ，连接AD，则∠BAD=∠BFD，即可求线段MG的长．
练习册系列答案
金钥匙试卷系列答案
相关题目
