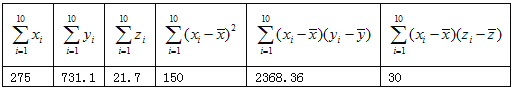题目内容
【题目】为了解学生的课外阅读时间情况，某学校随机抽取了50人进行统计分析，把这50人每天阅读的时间（单位：分钟）绘制成频数分布表，如下表所示：
阅读时间 | [0,20） | [20,40） | [40,60） | [60,80） | [80,100） | [100,120] |
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上（含60分钟）的同学称为“阅读达人”，根据统计结果中男女生阅读达人的数据，制作出如图所示的等高条形图：
（1）根据已知条件完成2x2列联表;
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
（2）并判断是否有
的把握认为“阅读达人”跟性别有关？
附：参考公式
【答案】（1）20；（2）见解析
【解析】分析：（1）根据频率分布表和等高条形图可得列联表．（2）根据列联表中的数据求得
，然后与临界值表中的数据对照可得结论．
详解：（1）由频数分布表得，“阅读达人”的人数是11+7+2=20人，
根据等高条形图得
列联表如下：
男生 | 女生 | 总计 | |
阅读达人 | 6 | 14 | 20 |
非阅读达人 | 18 | 12 | 30 |
总计 | 24 | 26 | 50 |
（2）由列联表可得
，
故没有
的把握认为“阅读达人”跟性别有关．
练习册系列答案
口算题天天练系列答案
相关题目
【题目】已知函数
的定义域为（0，+
），若
在（0，+）上为增函数，则称为“一阶比增函数”；若
在（0，+）上为增函数，则称为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为
1，所有“二阶比增函数”组成的集合记为2。
（1）已知函数
，若∈1，求实数
的取值范围，并证明你的结论；
（2）已知0<a<b<c，∈1且的部分函数值由下表给出：
|
|
|
|
|
|
|
| t | 4 |
求证：
；
（3）定义集合
，且存在常数k，使得任取x∈（0，+），<k}，请问：是否存在常数M，使得任意的∈
，任意的x∈（0，+），有<M成立?若存在，求出M的最小值；若不存在，说明理由。
