题目内容
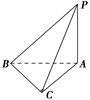
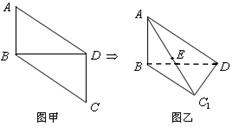
(本小题满分12分)如图所示,正方形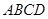 和矩形
和矩形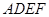 所在平面相互垂直,
所在平面相互垂直,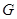 是
是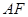 的中点.
的中点.
(1)求证: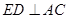 ;
;
(2)若直线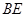 与平面
与平面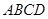 成45o角,求异面直线
成45o角,求异面直线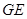 与
与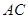 所成角的余弦值.
所成角的余弦值.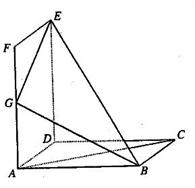
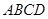 和矩形
和矩形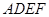 所在平面相互垂直,
所在平面相互垂直,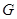 是
是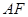 的中点.
的中点. (1)求证:
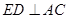 ;
;(2)若直线
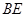 与平面
与平面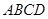 成45o角,求异面直线
成45o角,求异面直线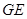 与
与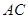 所成角的余弦值.
所成角的余弦值.
(I)证明:见解析;(Ⅱ)异面直线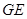 与
与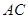 所成角的余弦值为
所成角的余弦值为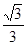 .
.
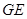 与
与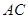 所成角的余弦值为
所成角的余弦值为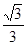 .
. 本题主要考查线线垂直,线面垂直,面面垂直间的转化以及异面直线所成的角的求法
(I)由矩形ADEF可知ED⊥AD,又因为平面ADEF⊥平面ABCD,得到ED⊥平面ABCD,从而有ED⊥AC.(Ⅱ)由(I)ED⊥平面ABCD,可知∠EDB是直线BE与平面ABCD所成的角,又由AM∥GE,知∠MAC是异面直线GE与AC所成角或其补角然后在△MAC中用余弦定理求解.
(I)证明:在矩形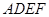 中,
中,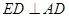
∵ 平面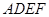
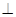 平面
平面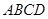 ,且平面
,且平面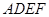
 平面
平面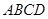
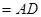
∴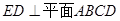 ∴
∴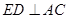 --------------6分
--------------6分
(Ⅱ)由(I)知: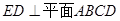
∴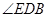 是直线
是直线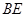 与平面
与平面 所成的角,即
所成的角,即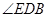
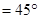 -----------8分
-----------8分
设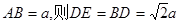 ,取
,取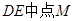 ,连接
,连接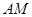 ∵
∵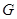 是
是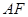 的中点
的中点
∴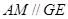 ∴
∴ 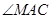 是异面直线
是异面直线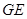 与
与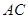 所成角或其补角--------10分
所成角或其补角--------10分
连接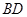 交
交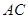 于点
于点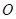 ∵
∵ 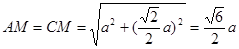 ,
,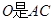 的中点
的中点
∴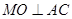 ∴
∴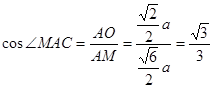
∴ 异面直线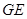 与
与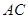 所成角的余弦值为
所成角的余弦值为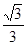 .-------12分
.-------12分
(I)由矩形ADEF可知ED⊥AD,又因为平面ADEF⊥平面ABCD,得到ED⊥平面ABCD,从而有ED⊥AC.(Ⅱ)由(I)ED⊥平面ABCD,可知∠EDB是直线BE与平面ABCD所成的角,又由AM∥GE,知∠MAC是异面直线GE与AC所成角或其补角然后在△MAC中用余弦定理求解.
(I)证明:在矩形
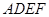 中,
中,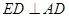
∵ 平面
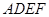
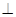 平面
平面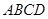 ,且平面
,且平面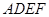
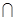 平面
平面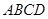
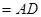
∴
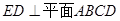 ∴
∴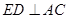 --------------6分
--------------6分(Ⅱ)由(I)知:
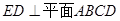
∴
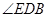 是直线
是直线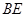 与平面
与平面 所成的角,即
所成的角,即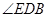
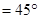 -----------8分
-----------8分设
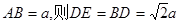 ,取
,取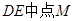 ,连接
,连接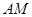 ∵
∵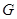 是
是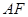 的中点
的中点 ∴
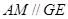 ∴
∴ 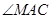 是异面直线
是异面直线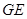 与
与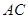 所成角或其补角--------10分
所成角或其补角--------10分连接
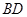 交
交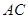 于点
于点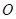 ∵
∵ 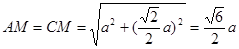 ,
,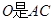 的中点
的中点∴
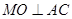 ∴
∴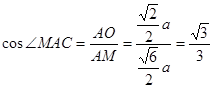
∴ 异面直线
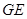 与
与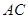 所成角的余弦值为
所成角的余弦值为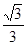 .-------12分
.-------12分
练习册系列答案
相关题目
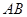 为圆
为圆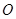 的直径,点
的直径,点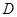 为线段
为线段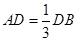 ,点
,点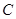 为圆
为圆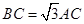 .点
.点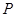 在圆
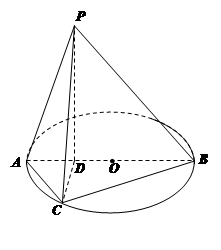
在圆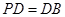 .
.
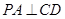 ;
;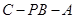 的余弦值.
的余弦值.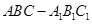 的侧棱与底面垂直,
的侧棱与底面垂直,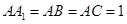 ,
,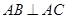 ,
,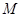 ,
,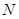 分别是
分别是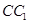 ,
,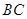 的中点,点
的中点,点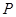 在直线
在直线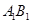 上,且
上,且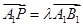 ;
;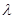 取何值,总有
取何值,总有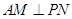 ;
;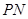 与平面
与平面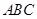 所成的角
所成的角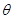 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;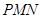 与平面
与平面
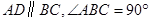 ,
,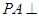 平面
平面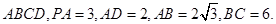
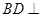 平面PAC;
平面PAC;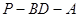 的大小.
的大小.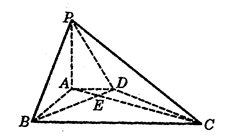
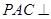 平面
平面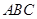 ,
,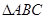 是以
是以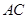 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,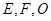 分别为
分别为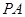 ,
,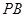 ,
,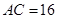 ,
,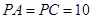 .
.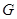 是
是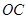 的中点,证明:
的中点,证明: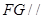 平面
平面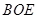 ;
;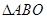 内是否存在一点
内是否存在一点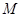 ,使
,使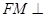 平面
平面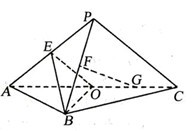
 ;(Ⅱ)求证:平面MAP⊥平面SAC;
;(Ⅱ)求证:平面MAP⊥平面SAC;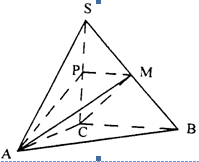
 外的两条直线,给出下列
外的两条直线,给出下列 ,则b∥
,则b∥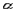 ,则
,则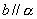 .则所有正确命题的序号是________.
.则所有正确命题的序号是________.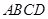 中,
中,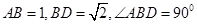 ,将它们沿对角线
,将它们沿对角线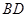 折起,折后的点
折起,折后的点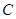 变为
变为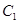 ,且
,且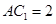 .
.
 平面
平面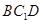 ;
;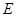 为线段
为线段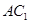 上的一个动点,当线段
上的一个动点,当线段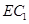 的长为多少时,
的长为多少时,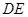 与平面
与平面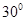 ?
?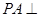 平面
平面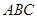 ,
,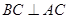 ,则图中直角三角形的个数为________.
,则图中直角三角形的个数为________.