题目内容
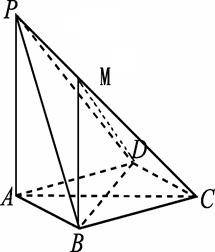
如图,在三棱锥S—ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设
PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
(I)求证: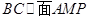 ;(Ⅱ)求证:平面MAP⊥平面SAC;
;(Ⅱ)求证:平面MAP⊥平面SAC;
( Ⅲ)求锐二面角M—AB—C的大小的余弦值;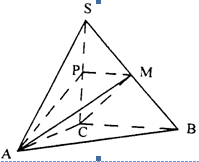
PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
(I)求证:
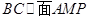 ;(Ⅱ)求证:平面MAP⊥平面SAC;
;(Ⅱ)求证:平面MAP⊥平面SAC;( Ⅲ)求锐二面角M—AB—C的大小的余弦值;

(I)见解析(Ⅱ)见解析( Ⅲ)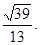
本试题主要是考查了空间中点线面的位置关系的综合运用。
(1)点P、M分别是SC和SB的中点 ∴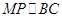
又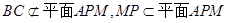 ∴
∴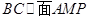
(2)建立空间直角坐标系C—xyz.,借助于法向量的垂直问题来证明面面的垂直。
(3)在第二问的基础上可知得到平面的法向量与法向量的夹角,得到二面角的平面角的大小。
解:(I)∵点P、M分别是SC和SB的中点 ∴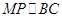
又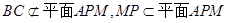 ∴
∴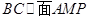
(II)∵SC⊥平面ABC,SC⊥BC,又∵∠ACB=90°
∴AC⊥BC,AC∩SC=C,BC⊥平面SAC, …………………………….2分
又∵P,M是SC、SB的中点
∴PM∥BC,PM⊥面SAC,∴面MAP⊥面SAC,……………………………..5分
(II)如图以C为原点建立如图所示空间直角坐标系C—xyz.
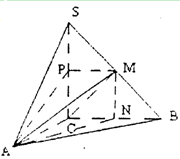
则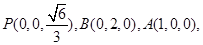
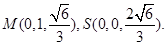
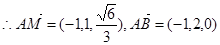 ………………………9分
………………………9分
设平面MAB的一个法向量为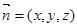 ,则
,则
由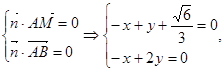 取z=
取z=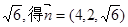 …………………..11分
…………………..11分
取平面ABC的一个法向量为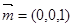
则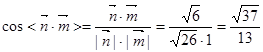
故二面角M—AB—C的余弦值为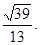 …………………….13分
…………………….13分
(1)点P、M分别是SC和SB的中点 ∴
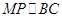
又
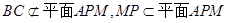 ∴
∴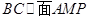
(2)建立空间直角坐标系C—xyz.,借助于法向量的垂直问题来证明面面的垂直。
(3)在第二问的基础上可知得到平面的法向量与法向量的夹角,得到二面角的平面角的大小。
解:(I)∵点P、M分别是SC和SB的中点 ∴
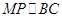
又
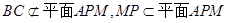 ∴
∴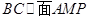
(II)∵SC⊥平面ABC,SC⊥BC,又∵∠ACB=90°
∴AC⊥BC,AC∩SC=C,BC⊥平面SAC, …………………………….2分
又∵P,M是SC、SB的中点
∴PM∥BC,PM⊥面SAC,∴面MAP⊥面SAC,……………………………..5分
(II)如图以C为原点建立如图所示空间直角坐标系C—xyz.

则
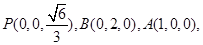
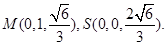
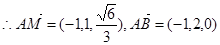 ………………………9分
………………………9分设平面MAB的一个法向量为
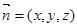 ,则
,则由
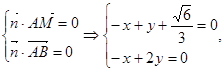 取z=
取z=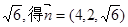 …………………..11分
…………………..11分取平面ABC的一个法向量为
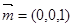
则
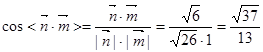
故二面角M—AB—C的余弦值为
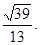 …………………….13分
…………………….13分
练习册系列答案
相关题目
 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是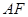 的中点.
的中点. 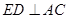 ;
;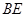 与平面
与平面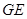 与
与 所成角的余弦值.
所成角的余弦值.
 ,
, 是底
是底 对角线的交点.
对角线的交点.
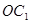 ∥面
∥面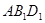 ;(2)
;(2)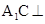 面
面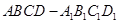 的面对角线
的面对角线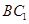 上运动,则下列四个命题:①三棱锥
上运动,则下列四个命题:①三棱锥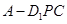 的体积不变; ②
的体积不变; ②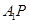 ∥面
∥面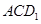 ; ③
; ③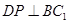 ; ④面
; ④面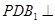 面
面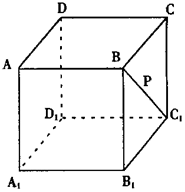
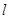 是直线,a,β是两个不同的平面
是直线,a,β是两个不同的平面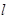 ⊥β
⊥β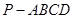 中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4,求二面角
中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4,求二面角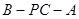 的余弦值.
的余弦值.
 与平面
与平面 所成角的正切值;
所成角的正切值; ,CM=3,求二面角
,CM=3,求二面角 的余弦值.
的余弦值.