题目内容
11.已知m∈R,设命题p:不等式|m2-m|>6;命题q:函数$f(x)={x^3}+m{x^2}+(m+\frac{4}{3})x+2$在(-∞,+∞)上有极值.求使p且q为真命题的m取值范围.分析 若p真,解绝对值不等式,求出m的范围,若q真,令f(x)的导函数的判别式大于0,求出m的范围,再根据复合命题真值表求出p真、q真时m的范围.
解答 解:若p为真命题,|m2-m|>6,
∴m2-m>6或m2-m<-6,
∴m>3或m<-2,
若q为真命题,|函数$f(x)={x^3}+m{x^2}+(m+\frac{4}{3})x+2$在(-∞,+∞)上有极值,
∴f'(x)=3x2+2mx+m+$\frac{4}{3}$=0有解,
∴△=4m2-12(m+$\frac{4}{3}$)>0.
解得m>4或m<-1,
根据复合命题真值表,若“P且q”为真命题,则命题P,命题q都是真命题,
则p∩q={m>4或m<-2}.
点评 该题重点考查了复合命题真假值表,另外又考了含绝对值不等式及一元二次不等次解法,在q命题真假的判断上有考查了导函数为二次函数的一元三次函数在实数集R存在极值的充要条.属于中档题.

练习册系列答案
相关题目
2.已知函数f(x)=$\frac{1}{2}$x2-x-2lnx,则函数f(x)的单调递增区间为( )
| A. | (-∞,-1)(2,+∞) | B. | (2,+∞) | C. | (-∞,-1) | D. | (-1,2) |
6.曲线y=ex上的点到直线y=x的距离的最小值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{e}{2}$ | D. | $\frac{{\sqrt{e}}}{2}$ |
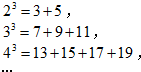 已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如:
已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如: