题目内容
6.曲线y=ex上的点到直线y=x的距离的最小值是( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{e}{2}$ | D. | $\frac{{\sqrt{e}}}{2}$ |
分析 设与直线y=x平行且与曲线y=ex相切于点P(x0,y0)的直线l的方程为:y=x+m.利用导数的几何意义可得x0=0,∴切点为P(0,1),求出点P到直线y=x的距离d即可.
解答 解:设与直线y=x平行且与曲线y=ex相切于点P(x0,y0)的直线l的方程为:y=x+m.
y′=ex,∴${e}^{{x}_{0}}$=1,解得x0=0,∴切点为P(0,1),
则点P到直线y=x的距离d=$\frac{|0-1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,即为所求的最小值.
故选:A.
点评 本题考查了导数的几何意义、相互平行的直线的距离,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知函数f(x)=sinx-$\sqrt{3}$cosx的定义域为[a,b],值域为[-1,2],则b-a的取值范围为( )
| A. | $[\frac{2π}{3},\frac{4π}{3}]$ | B. | $[{\frac{5π}{6},2π}]$ | C. | $[{\frac{7π}{6},\frac{5π}{3}}]$ | D. | $[{\frac{7π}{6},2π}]$ |
15.方程mx2+ny2=1不可能表示的曲线为( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
16.2014年国家加大对科技创新行业的支持力度,某研究机构对一新型行业的企业年投入x(单位:万元)与年盈利y(单位:万元)情况进行了统计分析,得下表数据:
根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=bx+a中的b的值为0.7,若某企业计划年投资14万元,则该企业的年盈利约为( )
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 6.5 | B. | 7 | C. | 7.5 | D. | 8 |
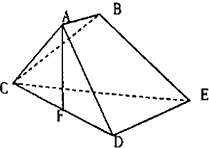 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.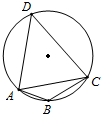 在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求:
在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求: