题目内容
2．设集合A={x|x2+2x-3＞0}，集合B={x|x2-2ax-1≤0，a＞0}．若A∩B中恰含有一个整数，则实数a的取值范围是[$\frac{3}{4}$，$\frac{4}{3}$）．分析 求出A中不等式的解集确定出A，由A与B交集中恰有一个整数，求出a的范围即可．
解答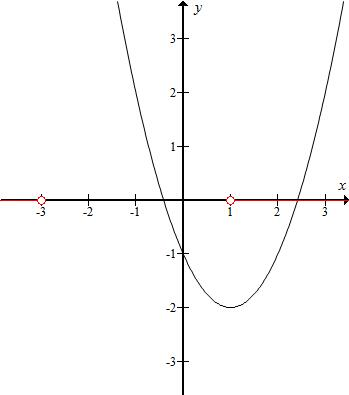 
，解：由A中不等式变形得：（x-1）（x+3）＞0，
解得：x＜-3或x＞1，即A={x|x＜-3或x＞1}，
函数y=f（x）=x2-2ax-1的对称轴为x=a＞0，f（-3）=6a+8＜0，
由对称性可得，要使A∩B恰有一个整数，
即这个整数解为2，
∴f（2）≤0且f（3）＞0，
即$\left\{\begin{array}{l}{4-4a-1≤0}\\{9-6a-1＞0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a≥\frac{3}{4}}\\{a＜\frac{4}{3}}\end{array}\right.$，即$\frac{3}{4}$≤a＜$\frac{4}{3}$，
则a的取值范围为[$\frac{3}{4}$，$\frac{4}{3}$）．
故答案为：[$\frac{3}{4}$，$\frac{4}{3}$）
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
12．已知两个等差数列{an}和{bn}的前n项和分别为Sn和Tn，且$\frac{S_n}{T_n}$=$\frac{2n+5}{n+3}$，则$\frac{a_5}{b_5}$为（ ）
| A． | $\frac{13}{7}$ | B． | $\frac{15}{8}$ | C． | $\frac{23}{12}$ | D． | $\frac{25}{13}$ |
10．已知F1和F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的两个焦点，A和B是以O为圆心，以|OF1|为半径的圆与该双曲线左支的两个交点，且△F2AB是等边三角形，则该双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{3}+1}}{2}$ | B． | $\sqrt{3}-1$ | C． | $\sqrt{3}+1$ | D． | 2 |
17．已知向量$\overrightarrow{a}$=（3，4），$\overrightarrow{b}$=（sinα，cosα），且$\overrightarrow{a}∥\overrightarrow{b}$，则tanα=（ ）
| A． | $\frac{3}{4}$ | B． | -$\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | -$\frac{4}{3}$ |
14．要得到函数y=sin（-$\frac{1}{3}$x）的图象，只需将函数y=sin（-$\frac{1}{3}$x+$\frac{π}{6}$）的图象（ ）
| A． | 向左平移$\frac{π}{2}$个单位 | B． | 向右平移$\frac{π}{2}$个单位 | ||
| C． | 向左平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |