题目内容
【题目】直线l1:ax﹣y+b=0,l2:bx+y﹣a=0(ab≠0)的图象只可能是图中的( )
A.
B.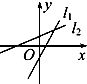
C.
D.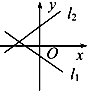
【答案】A
【解析】解:直线l1的方程是ax﹣y+b=0,可化为y=ax+b,l2的方程是bx+y﹣a=0,可化为y=﹣bx+a(ab≠0).
假设A选项直线l1正确:即斜率a>0,在y轴上的截距b<0.而直线l2的斜率﹣b>0,与图中符合,故A正确.
假设B选项直线l1正确:即斜率a>0,在y轴上的截距b>0.则图中直线l2的斜率为正,直线l2的﹣b<0,不满足题目条件,故B不正确.
假设C选项直线l1正确:即斜率a<0,在y轴上的截距b>0.则图中直线l2的斜率﹣b<0,与直线l2的斜率矛盾.故C不正确.
假设D选项直线l1正确:即斜率a<0,在y轴上的截距b<0.则图中直线l2的斜率满足题意,在y轴上的截距皆小于0,与解析式y=﹣bx+a(ab≠0,a≠b)中的焦距不相符.所以不正确.
综上可知只有A正确.
故选:A.

练习册系列答案
相关题目