��Ŀ����
����Ŀ�������ֵ����ĵ�����ȱ��������˾Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѰ취����ij������ÿ��Ӧ�����y��Ԫ�����õ���x���ȣ��ĺ���ͼ����һ�����ߣ���ͼ��ʾ��������ͼ����������⣺ 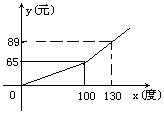
��1���ֱ�д����0��x��100��x��100ʱ��y��x�ĺ�����ϵʽ��
��2�����ú�����ϵʽ��˵��������˾��ȡ���շѱ���
��3�������û�ij���õ�62�ȣ���Ӧ�ɷѶ���Ԫ�������û�ij�½ɷ�105Ԫʱ������û��������˶��ٶȵ磿
���𰸡�
��1���⣺����100��65������y=kx�ã�100k=65���k=0.65
��y=0.65x��0��x��100��
����100��65������130��89������y=kx+b�ã� ![]() ���
��� ![]()
��y=0.8x��15��x��100���� ![]()
��2���⣺���ݣ�1���ĺ�����ϵʽ��
���õ�����0�ȵ�100��֮��ʱ��ÿ�ȵ���շѵı���0.65Ԫ��
���õ�������100��ʱ����������ÿ�ȵ���շѵı���0.8Ԫ
��3���⣺�û����õ�62��ʱ��62��0.65=4.03���û�Ӧ�ɷ�40.3Ԫ��
�û��½ɷ�105Ԫʱ����0.8x��15=105���x=150�����û���������150�ȵ�
����������1�����ú�����ͼ��ͨ���ֶκ�����⺯���Ľ���ʽ���ɣ���2�����÷ֶκ����ֱ���⺯������ֵ���ɣ�

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�