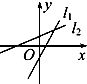题目内容
【题目】如图，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x﹣4．设圆C的半径为1，圆心在l上．
（1）若圆心C也在直线y=x﹣1上，过点A作圆C的切线，求切线的方程；
（2）若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围．
【答案】
（1）解：联立得： 
，
解得： 
，
∴圆心C（3，2）．
若k不存在，不合题意；
若k存在，设切线为：y=kx+3，可得圆心到切线的距离d=r，即 
=1，
解得：k=0或k=﹣ 
，
则所求切线为y=3或y=﹣ x+3
（2）解：设点M（x，y），由MA=2MO，知： 
=2 
，
化简得：x2+（y+1）2=4，
∴点M的轨迹为以（0，﹣1）为圆心，2为半径的圆，可记为圆D，
又∵点M在圆C上，C（a，2a﹣4），
∴圆C与圆D的关系为相交或相切，
∴1≤|CD|≤3，其中|CD|= 
，
∴1≤ ≤3，
解得：0≤a≤ 
【解析】（1）联立直线l与直线y=x﹣1解析式，求出方程组的解得到圆心C坐标，根据A坐标设出切线的方程，由圆心到切线的距离等于圆的半径，列出关于k的方程，求出方程的解得到k的值，确定出切线方程即可；（2）设M（x，y），由MA=2MO，利用两点间的距离公式列出关系式，整理后得到点M轨迹为以（0，﹣1）为圆心，2为半径的圆，可记为圆D，由M在圆C上，得到圆C与圆D相交或相切，根据两圆的半径长，得出两圆心间的距离范围，利用两点间的距离公式列出不等式，求出不等式的解集，即可得到a的范围．
阅读快车系列答案
【题目】对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计，做出甲的得分频率分布直方图如图所示，列出乙的得分统计表如表所示：
分值 | [0，10） | [10，20） | [20，30） | [30，40） |
场数 | 10 | 20 | 40 | 30 |
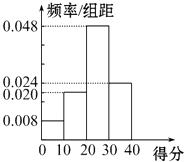
（1）估计甲在一场比赛中得分大于等于20分的概率．
（2）判断甲、乙两名运动员哪个成绩更稳定．（结论不要求证明）
（3）试利用甲的频率分布直方图估计甲每场比赛的平均得分．
【题目】某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：
A配方的频数分布表
指标值分组 | [90，94） | [94，98） | [98，102） | [102，106） | [106，110] |
频数 | 8 | 20 | 42 | 22 | 8 |
B配方的频数分布表
指标值分组 | [90，94） | [94，98） | [98，102） | [102，106） | [106，110] |
频数 | 4 | 12 | 42 | 32 | 10 |
（1）分别估计用A配方，B配方生产的产品的优质品率；
（2）已知用B配方生产的一件产品的利润y（单位：元）与其质量指标值t的关系式为y= 
估计用B配方生产的一件产品的利润大于0的概率，并求用B配方生产的上述100件产品平均一件的利润．
