Question

【题目】将边长为1的正方形ABCD沿对角线AC折起，使得平面ADC⊥平面ABC，在折起后形成的三棱锥D﹣ABC中，给出下列三个命题：
①△DBC是等边三角形；
②AC⊥BD；
③三棱锥D﹣ABC的体积是 ．
其中正确命题的序号是（写出所有正确命题的序号）

Answer 1

【答案】①②
【解析】解：如图所示：BD=
又BC=DC=1
∴面DBC是等边三角形①正确．
∵AC⊥DO，AC⊥BO
∴AC⊥平面DOB
∴AC⊥BD
②正确．
三棱锥D﹣ABC的体积=
③不正确．
所以答案是：①②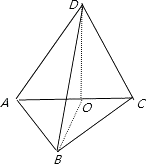

【考点精析】关于本题考查的棱锥的结构特征和平面的基本性质及推论，需要了解侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方；如果一条直线上的两点在一个平面内，那么这条直线在此平面内;过不在一条直线上的三点，有且只有一个平面;如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线才能得出正确答案．