题目内容
【题目】如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
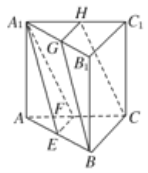
求证:(1)GH∥面ABC
(2)平面EFA1∥平面BCHG.
【答案】(1)见解析(2)见解析
【解析】
(1) 根据三角形中位线定理以及三棱柱的性质可推导出![]() ,由线面平行的判定定理能证明
,由线面平行的判定定理能证明![]() 面
面![]() ;(2)由三角形中位线定理推导出
;(2)由三角形中位线定理推导出![]() ,由平行四边形的性质可得
,由平行四边形的性质可得![]() ,从而可证明平面
,从而可证明平面![]() 平面
平面![]() .
.
(1)∵在三棱柱ABCA1B1C1中,
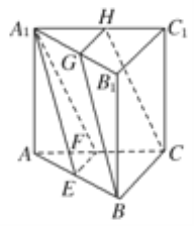
E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
∴GH∥B1C1∥BC,
∵GH平面ABC,BC平面ABC,
∴GH∥面ABC.
(2)∵在三棱柱ABCA1B1C1中,
E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
∴EF∥BC,A1G![]() BE,
BE,
∴四边形BGA1E是平行四边形,∴A1E∥BG,
∵A1E∩EF=E,BG∩BC=B,
A1E,EF平面EFA1,BG,BC平面BCHG,
∴平面EFA1∥平面BCHG.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目