题目内容
【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ![]() ,证明:
,证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*).
Sn+1(n∈N*).
【答案】
(1)解:设等比数列{an}的公比为q,
由an+1+an=104n﹣1(n∈N*),可得a1(1+q)qn﹣1=104n﹣1,
即有q=4,a1(1+q)=10,解得a1=2,
则an=24n﹣1=22n﹣1,bn=log2an=log222n﹣1=2n﹣1,
Sn= ![]() (1+2n﹣1)n=n2;
(1+2n﹣1)n=n2;
(2)证明:cn= ![]() =n,
=n,
不等式 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1,
Sn+1,
即为 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (n+1)2.
(n+1)2.
运用数学归纳法证明.
当n=1时,左边= ![]() ,右边=
,右边= ![]() ×4=2,不等式成立;
×4=2,不等式成立;
假设n=k时,不等式 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (k+1)2.
(k+1)2.
当n=k+1时, ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]()
< ![]() (k+1)2+
(k+1)2+ ![]() ,
,
要证 ![]() (k+1)2+
(k+1)2+ ![]() <
< ![]() (k+2)2.
(k+2)2.
即证 ![]() <
< ![]() (k+2)2﹣
(k+2)2﹣ ![]() (k+1)2=
(k+1)2= ![]() (2k+3),
(2k+3),
平方可得k2+3k+2<k2+3k+ ![]() ,即有2<
,即有2< ![]() 成立.
成立.
可得n=k+1时,不等式也成立.
综上可得, ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*)
Sn+1(n∈N*)
【解析】(1)设等比数列{an}的公比为q,运用等比数列的通项公式,可得首项为2,公比为4,可得an=22n﹣1 , 由对数的运算性质可得bn=2n﹣1,运用等差数列的求和公式即可得到Sn;(2)求得cn= ![]() =n,原不等式即为
=n,原不等式即为 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (n+1)2 . 运用数学归纳法证明.结合分析法,注意运用假设,化简整理,即可得证.
(n+1)2 . 运用数学归纳法证明.结合分析法,注意运用假设,化简整理,即可得证.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系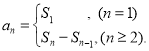 .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案