题目内容
【题目】对于函数①
，②
，③
，
判断如下两个命题的真假：
命题甲： 
在区间
上是增函数；
命题乙： 
在区间
上恰有两个零点
，且
.
能使命题甲、乙均为真的函数的序号是
A. ① B. ② C. ①③ D. ①②
【答案】D
【解析】①f’（x）=4﹣
，在区间（1，2）f’（x）＞0，f（x）在区间（1，2）上是增函数．使甲为真．f（x）的最小值是﹣1＜0当x=
时取得．又f（1）=0，∴f（x）在区间（0，+∞）上恰有两个零点x1＜；x2=1． x1x2=x1＜1，使乙为真．
②在区间（1，2），|log2x|=log2x，是增函数．﹣
也是增函数，两者的和函数也是增函数．使甲为真．利用信息技术f（x）在区间（0，+∞）上恰有两个零点x1，x2；0＜x1＜
1＜x2＜2．使乙为真．
③f（x）=0得cos（x+2）=cosx．x+2=2kπ±x．x=kπ﹣1，k∈Z，在区间（0，+∞）上有无数个零点．使乙为假．
故选D．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】假设关于某种设备的使用年限
(年)与所支出的维修费用
(万元)有如下统计：
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
. 
， 
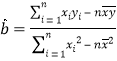(1)求
， 
；
(2)与具有线性相关关系，求出线性回归方程；
(3)估计使用年限为10年时，维修费用约是多少？
