题目内容
【题目】已知在长方体ABCD-A1B1C1D1中，AB=2，BC=2，CC1=3，长方体每条棱所在直线与过点C1的平面α所成的角都相等，则直线AC与平面α所成角的余弦值为（ ）
A. 
或1 B. 或0 C. 
或0 D. 或1
【答案】A
【解析】
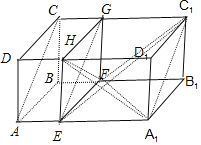
在长方体ABCD-A1B1C1D1中截取一个棱长为2的正方体EFGH-A1B1C1D1，要使长方体每条棱所在直线与过点C1的平面α所成的角都相等，则平面α可视为平面C1FA1及于平面HFA1平行的平面．利用正方体棱的关系，判断平面α所成的角都相等的位置，然后求解直线AC与平面α所成角的余弦值．
如图，在长方体ABCD-A1B1C1D1中截取一个棱长为2的正方体EFGH-A1B1C1D1，
长方体每条棱所在直线与过点C1的平面α所成的角都相等，则平面α可视为平面C1FA1及于平面HFA1平行的平面．
直线AC与平面C1FA1所成角=直线C1A1与平面C1FA1所成角=0，所以余弦值为1，
∵AC∥EG，EC1⊥面FHA1，∴直线AC与平面HFA1所成角的余弦值等于EG与EC1所成角∠GEC1的正弦值，
在直角△EGC1中，
，GC1＝2，
，
∴sin
．
∴直线AC与平面α所成角的余弦值为1，
，
故选：A．
练习册系列答案
相关题目
