题目内容
10．已知直线过点A（m，m），B（m-1，m+1），则直线AB的倾斜角为（ ）| A． | $\frac{π}{4}$ | B． | $-\frac{π}{4}$ | C． | $\frac{3π}{4}$ | D． | 以m的值有关 |
分析 先由题设条件求出直线AB的斜率k=$\frac{m+1-m}{m-1-m}$=-1，由此能求出直线AB的倾斜角．
解答 解：∵A（m，m），B（m-1，m+1），
∴直线AB的斜率k=$\frac{m+1-m}{m-1-m}$=-1，
∴直线AB的倾斜角α=$\frac{3π}{4}$．
故选C
点评 本题考查直线的倾斜角的求法，解题时要认真审题，注意直线的斜率公式的灵活运用．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
1．有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如下表：
根据以上数据，用线性回归的方法，求得销售额y与平均气温x之间回归直线方程$\widehat{y}$=bx+a的系数$\widehat{b}$=-2.4，则预测平均气温为-8℃时该商品销售额为34.6万元．
| 平均气温（℃） | -2 | -3 | -5 | -6 |
| 销售额（万元） | 20 | 23 | 27 | 30 |
18．在直角坐标系xOy中，点M的坐标是（1，-$\sqrt{3}$），若以原点O为极点，x轴的非负半轴为极轴建立极坐标系，则点M的极坐标可以为（ ）
| A． | （2，$\frac{π}{3}$） | B． | （2，$\frac{2π}{3}$） | C． | （2，-$\frac{π}{3}$） | D． | （2，2kπ+$\frac{π}{3}$）（k∈Z） |
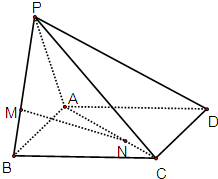如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，侧面PAB是边长为3的等边三角形，底面ABCD是正方形，M是侧棱PB上的点，N是底面对角线AC上的点，且PM=2MB，AN=2NC．