题目内容
设α为平面,a、b为两条不同的直线,则下列叙述正确的是( )
| A、若a∥α,b∥α,则a∥b | B、若a⊥α,a∥b,则b⊥α | C、若a⊥α,a⊥b,则b∥α | D、若a∥α,a⊥b,则b⊥α |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间线线、线面、面面间的关系求解.
解答:解:若a∥α,b∥α,则a与b相交、平行或异面,故A错误;
若a⊥α,a∥b,则由直线与平面垂直的判定定理知b⊥α,故B正确;
若a⊥α,a⊥b,则b∥α或b?α,故C错误;
若a∥α,a⊥b,则b∥α,或b?α,或b与α相交,故D错误.
故选:B.
若a⊥α,a∥b,则由直线与平面垂直的判定定理知b⊥α,故B正确;
若a⊥α,a⊥b,则b∥α或b?α,故C错误;
若a∥α,a⊥b,则b∥α,或b?α,或b与α相交,故D错误.
故选:B.
点评:本题考查命题的真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知f(x)=
,则关于F(x)=f(f(x))+a的零点个数,判断正确的是( )
|
| A、k<0时,若a≥e,则有2个零点 | ||
| B、k>0时,若a>e,则有4个零点 | ||
C、无论k为何值,若-
| ||
| D、k>0时,若0≤a<e,则有3个零点 |
三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )


A、2
| ||
B、4
| ||
C、
| ||
D、16
|
 如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为( )
如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为( )| A、π | B、2π | C、3π | D、4π |
已知平面α、β和直线m,给出条件:①m∥α;②m⊥α;③m?α;④α⊥β;⑤α∥β.由这五个条件中的两个同时成立能推导出m∥β的是( )
| A、①④ | B、①⑤ | C、②⑤ | D、③⑤ |
过点P(-1,3),且平行于直线2x-4y+1=0的直线方程为( )
| A、2x+y-5=0 | B、2x+y-1=0 | C、x-2y+7=0 | D、x-2y-5=0 |
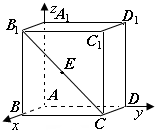 如图,已知正方体ABCD-A1B1C1D1棱长为2,E是线段B1C的中点,分别以AB、AD、AA1为x、y、z轴建立如图所示的空间直角坐标系A-xyz,点E的坐标是
如图,已知正方体ABCD-A1B1C1D1棱长为2,E是线段B1C的中点,分别以AB、AD、AA1为x、y、z轴建立如图所示的空间直角坐标系A-xyz,点E的坐标是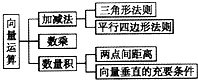 如图是向量运算的知识结构图,如果要加入“向量共线的充要条件”,则应该是在
如图是向量运算的知识结构图,如果要加入“向量共线的充要条件”,则应该是在