题目内容
过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,点O是坐标原点,则|AF|·|BF|的最小值是( )
| A.2 | B. | C.4 | D.2 |
C
解析试题分析:由抛物线的定义.抛物线上任一点到焦点的距离与到准线的距离是相等的.F(2,0),|AF|+|BF|=4.所以|AF|·|BF|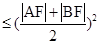 =4,故选C。
=4,故选C。
故填|BF|=2.
点评:活用圆锥曲线的定义是解决圆锥曲线最基本的方法.到焦点的距离,叫焦半径.到焦点的距离常转化到准线的距离求解.
考点:本题主要考查抛物线的定义及其标准方程。
点评:活用圆锥曲线的定义是解决圆锥曲线最基本的方法.到焦点的距离,叫焦半径.到焦点的距离常转化到准线的距离求解.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知直线 和直线
和直线 ,抛物线
,抛物线 上一动点
上一动点 到直线
到直线 和直线
和直线 的距离之和的最小值是 ( )
的距离之和的最小值是 ( )
| A.2 | B.3 | C. | D. |
对于直角坐标平面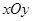 内的点
内的点 (不是原点),
(不是原点), 的“对偶点”
的“对偶点” 是指:满足
是指:满足 且在射线
且在射线 上的那个点. 则圆心在原点的圆的对偶图形( )
上的那个点. 则圆心在原点的圆的对偶图形( )
| A.一定为圆 | B.一定为椭圆 |
| C.可能为圆,也可能为椭圆 | D.既不是圆,也不是椭圆 |
双曲线 -
-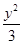 =1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
A. | B.2 | C.3 | D.6 |
已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点 到焦点的距离等于5,
到焦点的距离等于5,
则m
A. | B. | C. | D. |
设抛物线y2 = 8x的准线与x轴交于点Q,若过点Q的直线 与抛物线有公共点,则直线
与抛物线有公共点,则直线 的斜率的取值范围是( )
的斜率的取值范围是( )
A.[- , , ] ] | B.[-2 , 2 ] | C.[-1 , 1 ] | D.[-4 , 4 ] |
 的右焦点为
的右焦点为 ,右准线
,右准线  与两条渐近线交于
与两条渐近线交于 两点,如果
两点,如果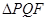 是等边三角形,则双曲线的离心率
是等边三角形,则双曲线的离心率 的值为( )
的值为( )


 与抛物线
与抛物线 的准线围成的三角形区域(包含边界)为
的准线围成的三角形区域(包含边界)为 ,
, 为
为 的最大值为( )
的最大值为( )



 ,动点P满足
,动点P满足 ,则点
,则点 的轨迹为( )
的轨迹为( )