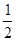题目内容
对于直角坐标平面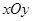 内的点
内的点 (不是原点),
(不是原点), 的“对偶点”
的“对偶点” 是指:满足
是指:满足 且在射线
且在射线 上的那个点. 则圆心在原点的圆的对偶图形( )
上的那个点. 则圆心在原点的圆的对偶图形( )
| A.一定为圆 | B.一定为椭圆 |
| C.可能为圆,也可能为椭圆 | D.既不是圆,也不是椭圆 |
A
解析试题分析:因为 满足
满足 且在射线
且在射线 上,所以
上,所以 到原点的距离为
到原点的距离为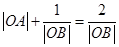 ,所以圆心在原点的圆上的点的对偶点到原点的距离均相等,所以圆心在原点的圆的对偶图形一定为圆.
,所以圆心在原点的圆上的点的对偶点到原点的距离均相等,所以圆心在原点的圆的对偶图形一定为圆.
考点:本小题主要考查新定义下圆的定义的理解和应用,考查学生理解新定义并合理转化的能力.
点评:圆、椭圆、双曲线和抛物线的定义在高考中经常考查,要合理转化,灵活应用.

练习册系列答案
相关题目
设抛物线的顶点在原点,焦点与椭圆 的右焦点重合,则此抛物线的方程是( )
的右焦点重合,则此抛物线的方程是( )
| A.y2=-8x | B.y2=-4x | C.y2="8x" | D.y2=4x |
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. | B. | C. | D.4 |
方程 所表示的曲线是( )
所表示的曲线是( )
| A.双曲线 | B.椭圆 | C.双曲线的一部分 | D.椭圆的一部分 |
过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,点O是坐标原点,则|AF|·|BF|的最小值是( )
| A.2 | B. | C.4 | D.2 |
命题甲:双曲线C的渐近线方程为y=± x;命题乙:双曲线C的方程为
x;命题乙:双曲线C的方程为 =1.那么甲是乙的( )
=1.那么甲是乙的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.不充分不必要条件 |
 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过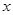 轴的直线与双曲线交于
轴的直线与双曲线交于 ,
, 两点,若△
两点,若△ 是锐角三角形,则该双曲线离心率的取值范围是( )
是锐角三角形,则该双曲线离心率的取值范围是( )



 的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且
的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且 ,则线段AB的中点坐标是( )
,则线段AB的中点坐标是( )