题目内容
设曲线 与抛物线
与抛物线 的准线围成的三角形区域(包含边界)为
的准线围成的三角形区域(包含边界)为 ,
, 为
为 内的一个动点,则目标函数
内的一个动点,则目标函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
C
解析试题分析:由题意画出可行域,由可行域可知,当目标函数 过点(1,-1)时有最大值,所以目标函数
过点(1,-1)时有最大值,所以目标函数 的最大值为8.
的最大值为8.
考点:抛物线的简单性质;线性规划的有关问题。
点评:求目标函数的最值,通常要把目标函数 转化为斜截式的形式,即
转化为斜截式的形式,即 的形式,但要注意
的形式,但要注意 的正负。当
的正负。当 为正时,求z的最大值就是求直线
为正时,求z的最大值就是求直线 在y轴上的截距最大时对应的点;当
在y轴上的截距最大时对应的点;当 为负时,求z的最大值就是求直线
为负时,求z的最大值就是求直线 在y轴上的截距最小时对应的点。
在y轴上的截距最小时对应的点。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
方程 所表示的曲线是( )
所表示的曲线是( )
| A.双曲线 | B.椭圆 | C.双曲线的一部分 | D.椭圆的一部分 |
过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,点O是坐标原点,则|AF|·|BF|的最小值是( )
| A.2 | B. | C.4 | D.2 |
双曲线 的渐近线与圆
的渐近线与圆 相切,则
相切,则 = ( )
= ( )
A. | B.2 | C.3 | D.6 |
命题甲:双曲线C的渐近线方程为y=± x;命题乙:双曲线C的方程为
x;命题乙:双曲线C的方程为 =1.那么甲是乙的( )
=1.那么甲是乙的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.不充分不必要条件 |
椭圆上 一动点P到两焦点距离之和为( )
一动点P到两焦点距离之和为( )
| A.10 | B.8 | C.6 | D.不确定 |
 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点 。若点
。若点 到该抛物线焦点的距离为
到该抛物线焦点的距离为 ,则
,则




 的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且
的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且 ,则线段AB的中点坐标是( )
,则线段AB的中点坐标是( )



 上一点
上一点 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线 的左顶点为
的左顶点为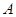 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线 平行,则实数
平行,则实数 的值是( )
的值是( )


