Question

【题目】某厂生产一种产品的固定成本(即固定投入)为0.5万元,但每生产一百件这样的产品,需要增加可变成本(即另增加投入)0.25万元. 市场对此产品的年需求量为500件,销售的收入函数为= (单位:万元),其中是产品售出的数量(单位:百件).

(1)该公司这种产品的年产量为百件,生产并销售这种产品所得到的利润为当年产量的函数,求;

(2)当年产量是多少时,工厂所得利润最大?

Answer 1

【答案】（1）=；（2）年产量500件时，工厂所得利润最大

【解析】试题分析：

(1)由题意将函数的解析式写成分段函数的形式： =；

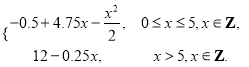(2)结合(1)中求得的函数解析式可得年产量500件时，工厂所得利润最大.

试题解析：

(1)利润=

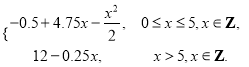
(2) 若则对称轴,

由,所以当x=5时y有最大值10.75.

若x>5,则是减函数,

所以,当x=6时y有最大值10.50.

综上:年产量500件时,工厂所得利润最大.