题目内容
【题目】直线l过定点P(0,1),且与直线l1:x-3y+10=0,l2:2x+y-8=0分别交于A、B两点.若线段AB的中点为P,求直线l的方程.
【答案】x+4y-4=0
【解析】解法一:设A(x0,y0),由中点公式,有B(-x0,2-y0),∵A在l1上,B在l2上,∴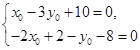
 ∴kAP=
∴kAP=![]() ,
,
故所求直线l的方程为y=![]() x+1,即x+4y-4=0.
x+1,即x+4y-4=0.
解法二:设所求直线l方程为y=kx+1,
由方程组![]() ,
,
由方程组![]() ,
,
∵A、B的中点为P(0,1),∴![]() ,∴k=
,∴k=![]() .
.
故所求直线l的方程为x+4y-4=0.
解法三:设A(x1,y1)、B(x2,y2),P(0,1)为MN的中点,则有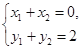
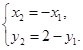 代入l2的方程,得2(-x1)+2-y1-8=0,即2x1+y1+6=0.由方程组
代入l2的方程,得2(-x1)+2-y1-8=0,即2x1+y1+6=0.由方程组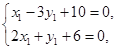 解得
解得 由两点式可得所求直线l的方程为x+4y-4=0.
由两点式可得所求直线l的方程为x+4y-4=0.
解法四:同解法一,设A(x0,y0),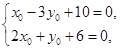 两式相减得x0+4y0-4=0,(1)
两式相减得x0+4y0-4=0,(1)
考察直线x+4y-4=0,一方面由(1)知A(x0,y0)在该直线上;另一方面P(0,1)也在该直线上,从而直线x+4y-4=0过点P、A.根据两点决定一条直线知,所求直线l的方程为x+4y-4=0.

练习册系列答案
相关题目



