题目内容
【题目】已知:函数f(x)= ![]() (a>0且a≠1).
(a>0且a≠1).
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)设a=![]() ,解不等式f(x)>0.
,解不等式f(x)>0.
【答案】(1) (-1,1);(2)见解析;(3) {x|-1<x<0}
【解析】试题分析:(I)根据对数函数有意义可知真数要大于0,列不等式组,解之即可求出函数的定义域;(Ⅱ)根据函数的奇偶性的定义进行判定,计箄![]() 与
与![]() 的关系,从而确定函数的奇偶性;(Ⅲ)将
的关系,从而确定函数的奇偶性;(Ⅲ)将![]() 代入,根据函数的定义域和函数的单调性列不等式组,解之即可求出
代入,根据函数的定义域和函数的单调性列不等式组,解之即可求出![]() 的范围.
的范围.
试题解析:(Ⅰ)由题知: ![]() ,解得:-1<x<1,所以函数f(x)的定义域为(-1,1);
,解得:-1<x<1,所以函数f(x)的定义域为(-1,1);
(Ⅱ)奇函数,
证明:因为函数f(x)的定义域为(-1,1),所以对任意x∈(-1,1),
f(-x)= ![]() =
=![]() =-f(x)
=-f(x)
所以函数f(x)是奇函数;
(Ⅲ)由题知: ![]() 即有
即有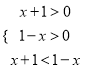 ,解得:-1<x<0,
,解得:-1<x<0,
所以不等式f(x)>0的解集为{x|-1<x<0}.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目