题目内容
【题目】设F为双曲线 ![]() ﹣
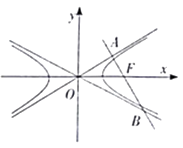
﹣ ![]() =1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( )
=1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( ) 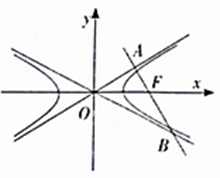
A.![]()
B.2
C.![]()
D.![]()
【答案】C
【解析】解:不妨设OA的倾斜角为锐角,
∵a>b>0,即0< ![]() <1,
<1,
∴渐近线l1的倾斜角为(0, ![]() ),
),
∴ ![]() =
= ![]() =e2﹣1<1,
=e2﹣1<1,
∴1<e2<2,
∵2|AB|=|OA|+|OB|,OA⊥AB,
∴|AB|2=|OB|2﹣|OA|2
=(|OB|﹣|OA|)(|OB|+|OA|)=2(|OB|﹣|OA|)|AB|,
∴|AB|=2(|OB|﹣|OA|),
∴|OB|﹣|OA|= ![]() |AB|,
|AB|,
又|OA|+|OB|=2|AB|,
∴|OA|= ![]() |AB|,
|AB|,
∴在直角△OAB中,tan∠AOB= ![]() =
= ![]() ,
,
由对称性可知:OA的斜率为k=tan( ![]() ∠AOB),
∠AOB),
∴ ![]() =
= ![]() ,∴2k2+3k﹣2=0,
,∴2k2+3k﹣2=0,
∴k= ![]() (k=﹣2舍去);
(k=﹣2舍去);
∴ ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() =e2﹣1=
=e2﹣1= ![]() ,
,
∴e2= ![]() ,
,
∴e= ![]() .
.
故选:C.

练习册系列答案
相关题目