题目内容
【题目】在正方体ABCD-A1B1C1D1中,如图.
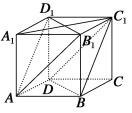
(1)求证:平面AB1D1∥平面C1BD;
(2)试找出体对角线A1C与平面AB1D1和平面C1BD的交点E,F,并证明:A1E=EF=FC.
【答案】略
【解析】证明:(1)因为在正方体ABCD-A1B1C1D1中,AD![]() B1C1,所以四边形AB1C1D是平行四边形,所以AB1∥C1D.又因为C1D
B1C1,所以四边形AB1C1D是平行四边形,所以AB1∥C1D.又因为C1D![]() 平面C1BD,AB1
平面C1BD,AB1![]() 平面C1BD,所以AB1∥平面C1BD.同理,B1D1∥平面C1BD.又因为AB1∩B1D1=B1,AB1
平面C1BD,所以AB1∥平面C1BD.同理,B1D1∥平面C1BD.又因为AB1∩B1D1=B1,AB1![]() 平面AB1D1,B1D1
平面AB1D1,B1D1![]() 平面AB1D1,所以平面AB1D1∥平面C1BD.
平面AB1D1,所以平面AB1D1∥平面C1BD.
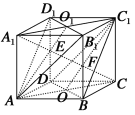
(2)如图,设A1C1与B1D1交于点O1,连接AO1,与A1C交于点E.
因为AO1![]() 平面AB1D1,
平面AB1D1,
所以点E也在平面AB1D1内,所以点E就是A1C与平面AB1D1的交点.
连接AC交BD于O,连接C1O与A1C交于点F,则点F就是A1C与平面C1BD的交点.
下面证明A1E=EF=FC.
因为平面A1C1CA∩平面AB1D1=EO1,平面A1C1CA∩平面C1BD=C1F,平面AB1D1∥平面C1BD,所以EO1∥C1F.
在△A1C1F中,O1是A1C1的中点,所以E是A1F的中点,
即A1E=EF.同理,CF=FE,所以A1E=EF=FC.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数).现随机抽取20天的指数(见下表),将指数不低于8.5视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
(Ⅰ)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(Ⅱ)以这20天的数据估计我市总体空气质量(天数很多).若从我市总体空气质量指数中随机抽取3天的指数,用X表示抽到空气质量为优良的天数,求X的分布列及数学期望.