题目内容
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
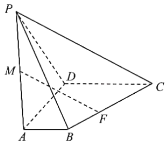
(I)求证:![]() ;
;
(II)求二面角_____的余弦值;
从①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
(III)若![]() 是棱
是棱![]() 的中点,求证:对于棱
的中点,求证:对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
【答案】(I)见解析(II)见解析(III)见解析
【解析】
(I)根据面面垂直的性质及线面垂直的判定定理,可证明![]() 平面
平面![]() ,进而证明
,进而证明![]() ;
;
(II)在平面![]() 内过点D作
内过点D作![]() ,交
,交![]() 于H,以D为原点,
于H,以D为原点,![]() 所在直线分别为x,y,z轴,建立空间直角坐标系
所在直线分别为x,y,z轴,建立空间直角坐标系![]() ,写出各个点的坐标,并求得各平面法向量,由法向量法即可求得各二面角的大小;
,写出各个点的坐标,并求得各平面法向量,由法向量法即可求得各二面角的大小;
(III)假设棱BC上存在点F,![]() .设
.设![]() 表示出
表示出![]() ,
,![]() ,设
,设![]() ,可得关于
,可得关于![]() 的方程组,方程组无解即可确定
的方程组,方程组无解即可确定![]() 与
与![]() 不平行.
不平行.
(I)证明:因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)选择①:在平面![]() 内过点D作
内过点D作![]() ,交
,交![]() 于H.
于H.
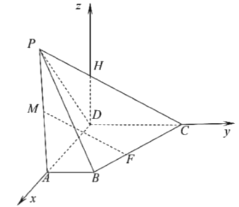
由(I)可知,![]() 平面
平面![]() ,所以
,所以![]() .
.
故![]() 两两垂直,
两两垂直,
如图,以D为原点,![]() 所在直线分别为x,y,z轴,建立空间直角坐标系
所在直线分别为x,y,z轴,建立空间直角坐标系![]() ,
,
则![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
而![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]()
则由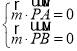 ,得
,得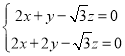 ,
,
取![]() ,有
,有![]() .
.
所以![]() .
.
由题知二面角![]() 为锐角,
为锐角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.
选择②:(下面给出关键点供参考,若与上面建系相同,)
平面ABCD的一个法向量为![]() ;
;
平面PBD的一个法向量为![]() ;
;
二面角![]() 为钝角:二面角
为钝角:二面角![]() 的余弦值为
的余弦值为![]() .
.
选择③:(下面给出关键点供参考,若与上面建系相同,)
平面ABCD的法向量![]() ;
;
平面PBC的法向量![]() ;
;
二面角![]() 为锐角;二面角
为锐角;二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)假设棱BC上存在点F,![]() .设
.设![]() .
.
依题意,可知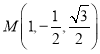 ,
,![]() ,
,
![]() ,
,![]() ,
,
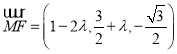 ,
,![]() ,设
,设![]() ,
,
则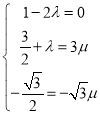 ,而此方程组无解,
,而此方程组无解,
故假设不成立,所以结论成立.

练习册系列答案
相关题目