题目内容
已知四棱锥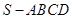 的底面为正方形且侧棱长与底面边长相等,
的底面为正方形且侧棱长与底面边长相等,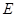 是
是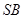 的中点,则
的中点,则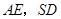 所成的角的余弦值为______
所成的角的余弦值为______
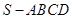 的底面为正方形且侧棱长与底面边长相等,
的底面为正方形且侧棱长与底面边长相等,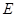 是
是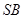 的中点,则
的中点,则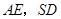 所成的角的余弦值为______
所成的角的余弦值为______
分析:由于是正方体,又是求角问题,所以易选用向量量,所以建立如图所示坐标系,先求得相关点的坐标,进而求得相关向量的坐标,最后用向量夹角公式求解.
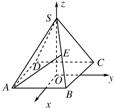
解:建立如图所示坐标系,
令正四棱锥的棱长为2,则A(1,-1,0),D(-1,-1,0),
S(0,0,
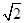 ),E(
),E(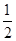 ,
,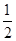 ,
,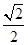 ),
),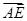 =(-
=(-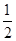 ,
,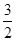 ,
,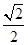 ),
),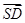 =(-1,-1,-
=(-1,-1,-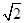 )
)∴cos<
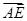 ,
,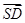 >=
>=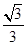

练习册系列答案
相关题目
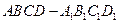 中,
中,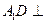 平面
平面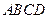 ,底面
,底面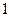 的正方形,侧棱
的正方形,侧棱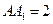 .
.
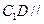 平面
平面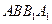 ;
;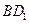 与平面
与平面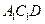 所成角的正弦值.
所成角的正弦值.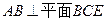 ,
,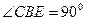 . 点
. 点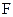 是
是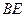 的中点. 求证:
的中点. 求证: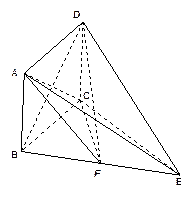
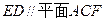
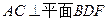
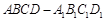 中,动点
中,动点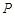 在
在 内,且到直线
内,且到直线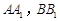 的距离之和等于
的距离之和等于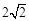 ,则
,则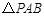 的面积最大值是 ( )
的面积最大值是 ( )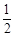
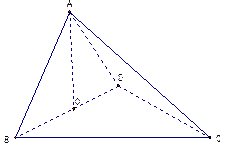
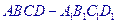 ,
,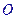 是底
是底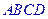 对角线的交点.
对角线的交点.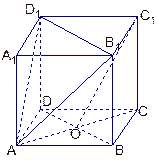
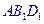 ;
;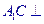 面
面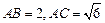 .
.
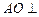 平面BCD;
平面BCD;  的底面ABCD是正方形,侧棱
的底面ABCD是正方形,侧棱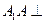 底面ABCD,E、F分别是C1D1,C1B1的中点,G为CC1上任一点
底面ABCD,E、F分别是C1D1,C1B1的中点,G为CC1上任一点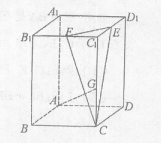
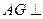 平面CEF,并说明理由;
平面CEF,并说明理由;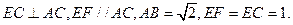

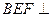 平
平 面DEF;
面DEF; 角A—BF—E的大小。
角A—BF—E的大小。