题目内容
(本小题满分12分)
如图,四棱柱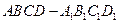 中,
中,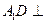 平面
平面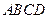 ,底面
,底面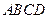 是边长为
是边长为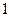 的正方形,侧棱
的正方形,侧棱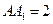 .
.

(1)求证: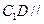 平面
平面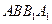 ;
;
(2)求直线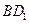 与平面
与平面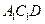 所成角的正弦值.
所成角的正弦值.
如图,四棱柱
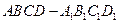 中,
中,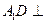 平面
平面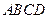 ,底面
,底面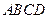 是边长为
是边长为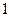 的正方形,侧棱
的正方形,侧棱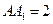 .
.
(1)求证:
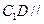 平面
平面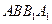 ;
;(2)求直线
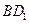 与平面
与平面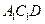 所成角的正弦值.
所成角的正弦值.(1)证明:四棱柱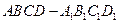 中,
中,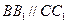 ,
,
又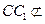 面
面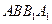 ,所以
,所以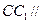 平面
平面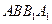 , ………………2分
, ………………2分
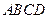 是正方形,所以
是正方形,所以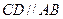 ,
,
又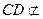 面
面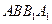 ,所以
,所以 平面
平面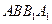 , ………………3分
, ………………3分
所以平面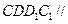 平面
平面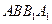 ,
,
所以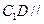 平面
平面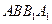 . ………………5分
. ………………5分
(2)解: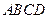 是正方形,
是正方形,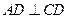 ,
,
因为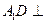 平面
平面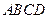 ,
,
所以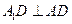 ,
,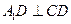 ,
,
如图,以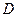 为原点建立空间直角坐标系
为原点建立空间直角坐标系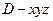 ,. ………………6分
,. ………………6分

在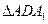
 中,由已知可得
中,由已知可得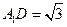 ,
,
所以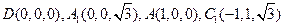 ,
,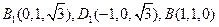 ,
,
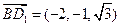 , …………………
, ………………… …………………………………………8分
…………………………………………8分
因为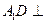 平面
平面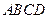 ,
,
所以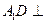 平面
平面 ,
,
 ,
,
又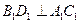 ,
,
所以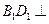 平面
平面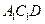 ,
,
所以平面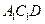 的一个法向量为
的一个法向量为
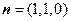 , …………………10分
, …………………10分
设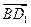 与
与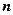 所成的角为
所成的角为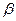 ,又
,又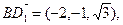 则
则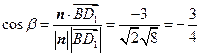 .
.
所以直线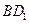 与平面
与平面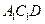 所成角的正弦值为
所成角的正弦值为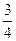 . ……………12分
. ……………12分
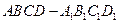 中,
中,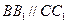 ,
,又
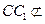 面
面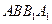 ,所以
,所以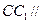 平面
平面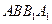 , ………………2分
, ………………2分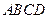 是正方形,所以
是正方形,所以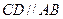 ,
,又
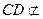 面
面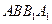 ,所以
,所以 平面
平面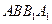 , ………………3分
, ………………3分所以平面
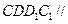 平面
平面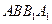 ,
,所以
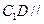 平面
平面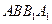 . ………………5分
. ………………5分(2)解:
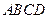 是正方形,
是正方形,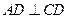 ,
,因为
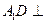 平面
平面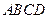 ,
,所以
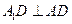 ,
,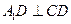 ,
, 如图,以
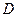 为原点建立空间直角坐标系
为原点建立空间直角坐标系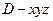 ,. ………………6分
,. ………………6分
在
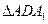
 中,由已知可得
中,由已知可得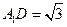 ,
,
所以
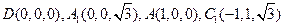 ,
,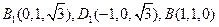 ,
,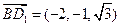 , …………………
, ………………… …………………………………………8分
…………………………………………8分因为
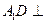 平面
平面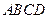 ,
,所以
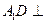 平面
平面 ,
, ,
,又
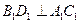 ,
,所以
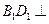 平面
平面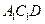 ,
, 所以平面
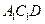 的一个法向量为
的一个法向量为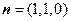 , …………………10分
, …………………10分设
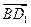 与
与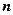 所成的角为
所成的角为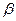 ,又
,又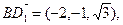 则
则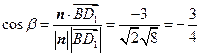 .
. 所以直线
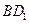 与平面
与平面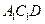 所成角的正弦值为
所成角的正弦值为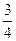 . ……………12分
. ……………12分略

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 中,
中,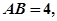 沿对角线
沿对角线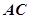 将正方形
将正方形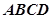 折成一个直二面角
折成一个直二面角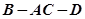 ,则点
,则点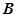 到直线
到直线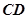 的距离为( )
的距离为( )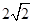
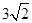
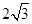
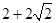
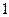 的正方体
的正方体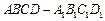 中,
中,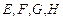 分别是棱
分别是棱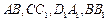 的中点.
的中点.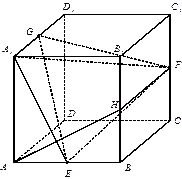
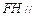 平面
平面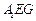 ;
;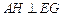 ;
;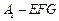 的体积.
的体积.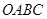 的三条棱
的三条棱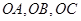 两两垂直,
两两垂直,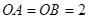 ,
,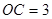 ,
,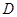 为四面体
为四面体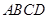 有三个面是直角三角形
有三个面是直角三角形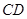 与
与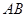 垂直并且相等
垂直并且相等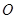 在四面体
在四面体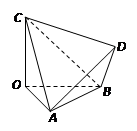
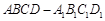 中,棱长都相等;条件乙:直四棱柱
中,棱长都相等;条件乙:直四棱柱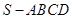 的底面为正方形且侧棱长与底面边长相等,
的底面为正方形且侧棱长与底面边长相等,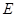 是
是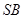 的中点,则
的中点,则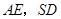 所成的角的余弦值为______
所成的角的余弦值为______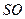 中,
中,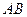 、
、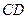 为底面圆的两条直径,
为底面圆的两条直径,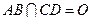 ,且
,且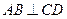 ,
,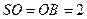 ,
,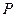 为
为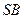 的中点.异面直线
的中点.异面直线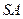 与
与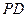 所成角的正切值为 .
所成角的正切值为 .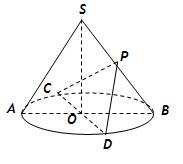
 (本小题满分12分)
(本小题满分12分)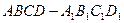 的下底面
的下底面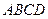 是边长为
是边长为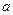 的正方形,
的正方形,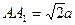 ,且点
,且点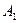 在下底面
在下底面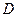 点.
点.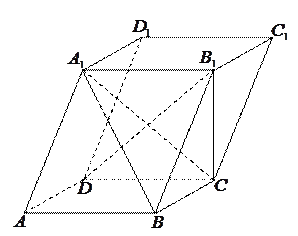
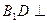 面
面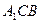 ;
;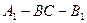 的大小.
的大小.