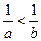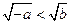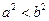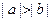题目内容
已知：m＞n，a＜b，求证：m－a＞n－b.
证明略
以不等式的性质为基础，进行推导
证法一：由m＞n知m－n＞0，由a＜b知b－a＞0.
∴（m－a）－（n－b）＝（m－n）＋（b－a）＞0
m－a＞n－b；
证法二：∵a＜b ∴－a＞－b
又∵m＞n ∴m＋（－a）＞n＋（－b）
∴m－a＞n－b.
证法一：由m＞n知m－n＞0，由a＜b知b－a＞0.
∴（m－a）－（n－b）＝（m－n）＋（b－a）＞0
m－a＞n－b；证法二：∵a＜b ∴－a＞－b
又∵m＞n ∴m＋（－a）＞n＋（－b）
∴m－a＞n－b.
练习册系列答案
相关题目
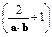成立
，高为2m的长方体纸盒，底面的长与宽取什么值时用纸最少？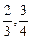
］，那么λ为何值时，能使宣传画所用纸张面积最小？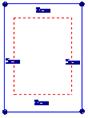
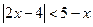
②
③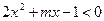
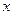值也满足③，求m的取值范围；
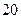分）设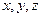
为非负实数，满足
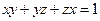，证明：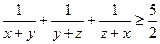
．
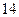
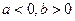，那么，下列不等式中正确的是（ ）
