题目内容
(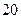 分)设
分)设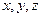 为非负实数,满足
为非负实数,满足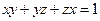 ,证明:
,证明: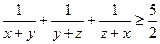 .
.
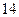
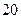 分)设
分)设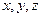 为非负实数,满足
为非负实数,满足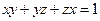 ,证明:
,证明: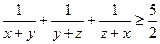 .
.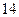
略
:为使所证式有意义,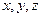 三数中至多有一个为
三数中至多有一个为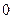 ;据对称性,不妨设
;据对称性,不妨设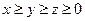 ,则
,则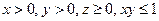 ;
;
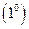 、当
、当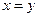 时,条件式成为
时,条件式成为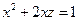 ,
,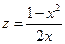 ,
,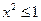 ,而
,而
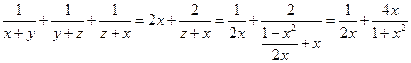 ,
,
只要证,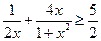 ,即
,即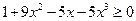 ,也即
,也即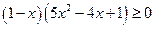 ,此为显然;取等号当且仅当
,此为显然;取等号当且仅当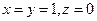 .
.
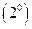 、再证,对所有满足
、再证,对所有满足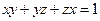 的非负实数
的非负实数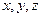 ,皆有
,皆有
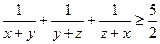 .显然,三数
.显然,三数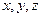 中至多有一个为
中至多有一个为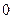 ,据对称性,
,据对称性,
仍设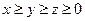 ,则
,则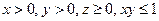 ,令
,令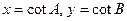 ,
,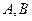 为锐角,以
为锐角,以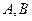 为内角,构作
为内角,构作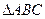 ,则
,则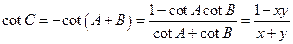
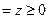 ,于是
,于是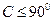 ,且由
,且由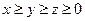 知,
知,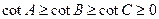 ;于是
;于是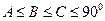 ,即
,即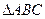 是一个非钝角三角形.
是一个非钝角三角形.
下面采用调整法,对于任一个以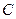 为最大角的非钝角三角形
为最大角的非钝角三角形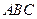 ,固定最大角
,固定最大角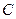 ,将
,将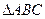 调整为以
调整为以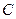 为顶角的等腰
为顶角的等腰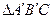 ,其中
,其中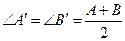 ,且设
,且设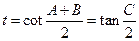 ,记
,记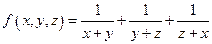 ,据
,据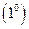 知,
知,
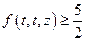 .今证明,
.今证明,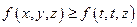 .即
.即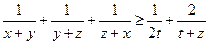 ……1.
……1.
即要证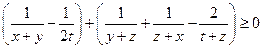 ……2
……2
先证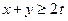 ……3,即证
……3,即证 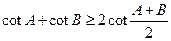 ,
,
即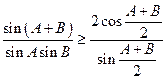 ,此即
,此即 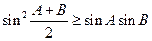 ,也即
,也即
 ,即
,即 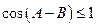 ,此为显然.
,此为显然.
由于在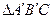 中,
中,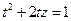 ,则
,则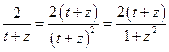 ;而在
;而在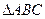 中,
中,
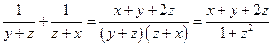 ,因此2式成为
,因此2式成为
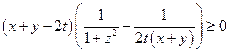 ……4,
……4,
只要证,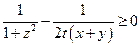 ……5,即证
……5,即证 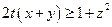 ,注意3式以及
,注意3式以及
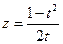 ,只要证
,只要证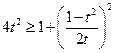 ,即
,即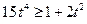 ,也即
,也即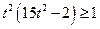 …6
…6
由于最大角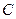 满足:
满足: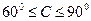 ,而
,而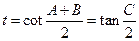 ,则
,则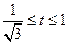 ,所以
,所以
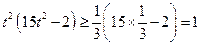 ,故6成立,因此5得证,由3及5得4成立,从而1成立,即
,故6成立,因此5得证,由3及5得4成立,从而1成立,即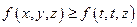 ,因此本题得证.
,因此本题得证.
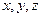 三数中至多有一个为
三数中至多有一个为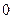 ;据对称性,不妨设
;据对称性,不妨设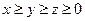 ,则
,则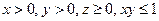 ;
;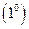 、当
、当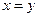 时,条件式成为
时,条件式成为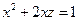 ,
,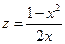 ,
,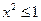 ,而
,而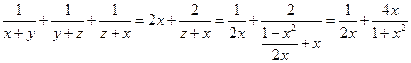 ,
,只要证,
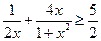 ,即
,即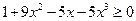 ,也即
,也即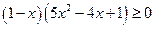 ,此为显然;取等号当且仅当
,此为显然;取等号当且仅当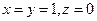 .
.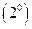 、再证,对所有满足
、再证,对所有满足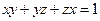 的非负实数
的非负实数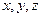 ,皆有
,皆有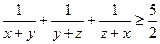 .显然,三数
.显然,三数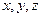 中至多有一个为
中至多有一个为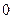 ,据对称性,
,据对称性,仍设
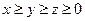 ,则
,则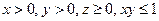 ,令
,令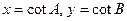 ,
,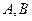 为锐角,以
为锐角,以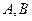 为内角,构作
为内角,构作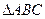 ,则
,则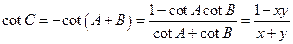
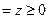 ,于是
,于是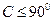 ,且由
,且由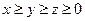 知,
知,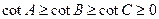 ;于是
;于是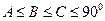 ,即
,即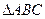 是一个非钝角三角形.
是一个非钝角三角形.下面采用调整法,对于任一个以
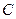 为最大角的非钝角三角形
为最大角的非钝角三角形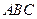 ,固定最大角
,固定最大角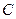 ,将
,将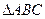 调整为以
调整为以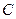 为顶角的等腰
为顶角的等腰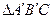 ,其中
,其中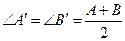 ,且设
,且设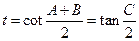 ,记
,记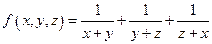 ,据
,据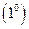 知,
知,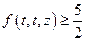 .今证明,
.今证明,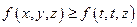 .即
.即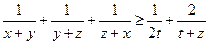 ……1.
……1.即要证
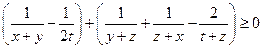 ……2
……2先证
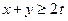 ……3,即证
……3,即证 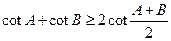 ,
,即
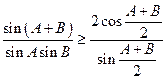 ,此即
,此即 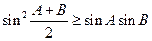 ,也即
,也即 ,即
,即 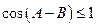 ,此为显然.
,此为显然.由于在
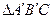 中,
中,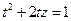 ,则
,则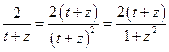 ;而在
;而在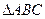 中,
中,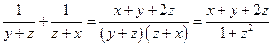 ,因此2式成为
,因此2式成为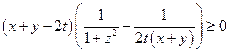 ……4,
……4,只要证,
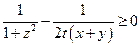 ……5,即证
……5,即证 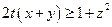 ,注意3式以及
,注意3式以及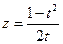 ,只要证
,只要证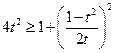 ,即
,即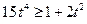 ,也即
,也即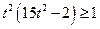 …6
…6由于最大角
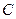 满足:
满足: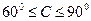 ,而
,而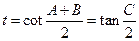 ,则
,则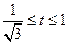 ,所以
,所以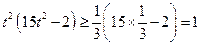 ,故6成立,因此5得证,由3及5得4成立,从而1成立,即
,故6成立,因此5得证,由3及5得4成立,从而1成立,即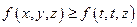 ,因此本题得证.
,因此本题得证.
练习册系列答案
相关题目
 -
-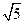 >
>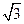
 +
+
 >3+
>3+
 >8
>8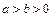 ,则下列不等式中总成立的是
,则下列不等式中总成立的是


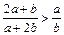
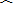
 的不等式
的不等式 的解集为
的解集为 ,则
,则 的范围是____
的范围是____