题目内容
己知三个不等式:①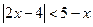
 ②
② ③
③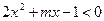
(1)若同时满足①、②的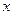 值也满足③,求m的取值范围;
值也满足③,求m的取值范围;
(2)若满足的③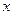 值至少满足①和②中的一个,求m的取值范围。
值至少满足①和②中的一个,求m的取值范围。
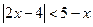
 ②
② ③
③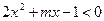
(1)若同时满足①、②的
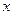 值也满足③,求m的取值范围;
值也满足③,求m的取值范围;(2)若满足的③
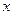 值至少满足①和②中的一个,求m的取值范围。
值至少满足①和②中的一个,求m的取值范围。(1)
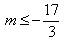
(2)
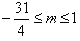
本例主要综合复习整式、分式不等式和含绝对值不等的解法,以及数形结合思想,解本题的关键弄清同时满足①、②的
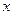 值的满足③的充要条件是:③对应的方程的两根分别在
值的满足③的充要条件是:③对应的方程的两根分别在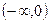 和
和 内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。
内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。解:记①的解集为A,②的解集为B,③的解集为C。
解①得A=(-1,3);解②得B=
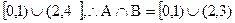
(1) 因同时满足①、②的
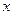 值也满足③,A
值也满足③,A B
B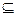 C
C设
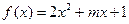 ,由
,由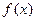 的图象可知:方程的小根小于0,大根大于或等于3时,即可满足
的图象可知:方程的小根小于0,大根大于或等于3时,即可满足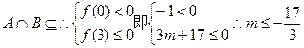
(2) 因满足③的
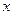 值至少满足①和②中的一个,
值至少满足①和②中的一个,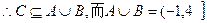 因
因此
 小根大于或等于-1,大根小于或等于4,因而
小根大于或等于-1,大根小于或等于4,因而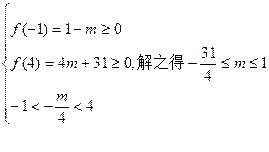
说明:同时满足①②的x值满足③的充要条件是:③对应的方程2x
 +mx-1=0的两根分别在(-∞,0)和[3,+∞)内,因此有f(0)<0且f(3)≤0,否则不能对A∩B中的所有x值满足条件.不等式和与之对应的方程及图象是有着密不可分的内在联系的,在解决问题的过程中,要适时地联系它们之间的内在关系.
+mx-1=0的两根分别在(-∞,0)和[3,+∞)内,因此有f(0)<0且f(3)≤0,否则不能对A∩B中的所有x值满足条件.不等式和与之对应的方程及图象是有着密不可分的内在联系的,在解决问题的过程中,要适时地联系它们之间的内在关系.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有两个相异实根,其中一根在区间
有两个相异实根,其中一根在区间 内,另一根在区间
内,另一根在区间 内,则
内,则 的取值范围是 。
的取值范围是 。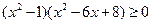
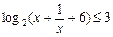 的解集为
的解集为  ,则下列不等式中总成立的是
,则下列不等式中总成立的是


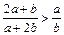
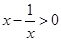 成立的充分不必要条件是
成立的充分不必要条件是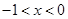 或
或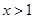 B.
B.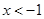 或
或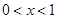 C.
C.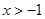 D.
D. 的图象经过点
的图象经过点 和
和 两点,
两点, ,则
,则 的取值范围是 ( )
的取值范围是 ( )



 的不等式
的不等式 的解集为
的解集为 ,则
,则 的范围是____
的范围是____