题目内容
已知－1＜a+b＜3且2＜a－b＜4，求2a+3b的取值范围.
－
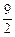＜2a+3b＜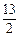
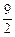＜2a+3b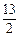＜∵a+b，a－b的范围已知，
∴要求2a+3b的取值范围，
只需将2a+3b用已知量a+b，a－b表示出来.
可设2a+3b=x（a+b）+y（a－b），用待定系数法求出x、y.
设2a+3b=x（a+b）+y（a－b），
∴
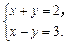解得
∴－
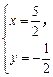
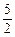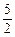＜（a+b）＜
，
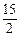－2＜－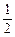
（a－b）＜－1.
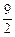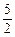∴－＜（a+b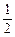）－（a－b）＜，
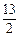即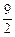－＜2a+3b＜.
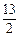错解：解此题常见错误是：－1＜a+b＜3， ①
2＜a－b＜4. ②
①+②得1＜2a＜7. ③
由②得－4＜b－a＜－2. ④
①+④得－5＜2b＜1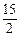，∴－＜3b＜
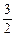. ⑤
③+⑤得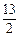－＜2a+3b＜
.
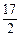∴要求2a+3b的取值范围，
只需将2a+3b用已知量a+b，a－b表示出来.
可设2a+3b=x（a+b）+y（a－b），用待定系数法求出x、y.
设2a+3b=x（a+b）+y（a－b），
∴
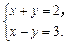解得∴－
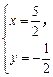
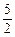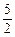＜（a+b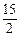）＜，－2＜－
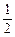（a－b）＜－1.∴－
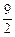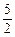＜（a+b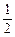）－（a－b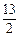）＜，即－
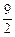＜2a+3b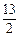＜.错解：解此题常见错误是：－1＜a+b＜3， ①
2＜a－b＜4. ②
①+②得1＜2a＜7. ③
由②得－4＜b－a＜－2. ④
①+④得－5＜2b＜1，∴－
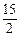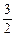＜3b＜. ⑤③+⑤得－
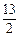＜2a+3b＜.
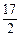练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
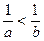成立的有( )
－
＞
＋
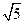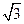
＞3＋
＞8
，求使函数值大于
的
的取值范围
)2千米，那么这批物资全部运到B市，最快需要_________小时(不计货车的车身长). 
的图象经过点
和
两点,
,则
的取值范围是 ( )
______时，函数
有最_______值，且最值是_________。