题目内容
已知a=(1,x),b=(x2+x,-x),m为常数且m≤-2,求使不等式a·b+2>m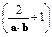 成立
成立
的x的范围.
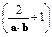 成立
成立的x的范围.
x的取值范围是(m,-2)∪(0,+∞)
∵a=(1,x),b=(x2+x,-x),
∴a·b=x2+x-x2=x.
由a·b+2>m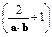
?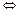 x+2>m
x+2>m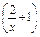
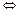 (x+2)-m
(x+2)-m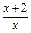 >0
>0
?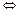 x(x+2)(x-m)>0(m≤-2).
x(x+2)(x-m)>0(m≤-2).
①当m=-2时,原不等式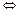 x(x+2)2>0
x(x+2)2>0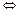 x>0;
x>0;
②当m<-2时,原不等式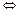 m<x<-2或x>0.
m<x<-2或x>0.
综上,得m=-2时,x的取值范围是(0,+∞);
m<-2时,x的取值范围是(m,-2)∪(0,+∞).
∴a·b=x2+x-x2=x.
由a·b+2>m
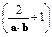
?
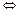 x+2>m
x+2>m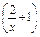
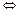 (x+2)-m
(x+2)-m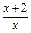 >0
>0?
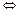 x(x+2)(x-m)>0(m≤-2).
x(x+2)(x-m)>0(m≤-2).①当m=-2时,原不等式
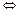 x(x+2)2>0
x(x+2)2>0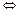 x>0;
x>0;②当m<-2时,原不等式
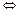 m<x<-2或x>0.
m<x<-2或x>0.综上,得m=-2时,x的取值范围是(0,+∞);
m<-2时,x的取值范围是(m,-2)∪(0,+∞).

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
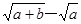 ,y=
,y=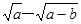 ,则x、y的大小关系为( )
,则x、y的大小关系为( )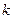 取什么值时,一元二次不等式
取什么值时,一元二次不等式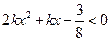 对一切实数
对一切实数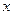 都成立?
都成立? 有两个相异实根,其中一根在区间
有两个相异实根,其中一根在区间 内,另一根在区间
内,另一根在区间 内,则
内,则 的取值范围是 。
的取值范围是 。 的解集不是空集,则实数a的取值范围是__________.
的解集不是空集,则实数a的取值范围是__________.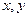 满足
满足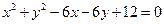 ,则
,则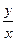 的最大值为
的最大值为 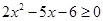 成立的一个充分不必要条件是
成立的一个充分不必要条件是