题目内容
设计一幅宣传画,要求画面面积为4840 cm2,画面的宽与高的比为λ(λ<1),画面的上、下各留8 cm的空白,左右各留5 cm空白,怎样确定画面的高与宽尺寸,才能使宣传画所用纸张面积最小?
如果要求λ∈[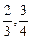 ],那么λ为何值时,能使宣传画所用纸张面积最小?
],那么λ为何值时,能使宣传画所用纸张面积最小?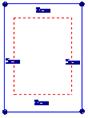
如果要求λ∈[
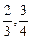 ],那么λ为何值时,能使宣传画所用纸张面积最小?
],那么λ为何值时,能使宣传画所用纸张面积最小?
画面高为88 cm,宽为55 cm时,所用纸张面积最小. 如果要求λ∈[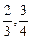 ],当λ=
],当λ=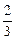 时,所用纸张面积最小。
时,所用纸张面积最小。
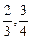 ],当λ=
],当λ=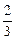 时,所用纸张面积最小。
时,所用纸张面积最小。 设画面高为x cm,宽为λx cm,则λx2=4840,设纸张面积为S cm2,
则S=(x+16)(λx+10)=λx2+(16λ+10)x+160,
将x=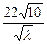 代入上式得
代入上式得 S=5000+44
S=5000+44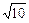 (8
(8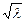 +
+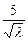 ),
),
当8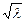 =
=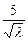 ,即λ=
,即λ=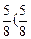 <1)时S取得最小值.
<1)时S取得最小值.
此时高: x=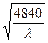 ="88" cm, 宽
="88" cm, 宽 λx=
λx=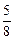 ×88="55" cm.
×88="55" cm.
如果λ∈[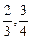 ],可设
],可设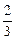 ≤λ1<λ2≤
≤λ1<λ2≤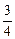 ,
,
则由S的表达式得:
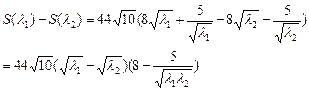
又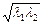 ≥
≥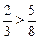 ,故8-
,故8-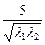 >0,
>0,
∴S(λ1)-S(λ2)<0,∴S(λ)在区间[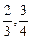 ]内单调递增。
]内单调递增。
从而对于λ∈[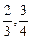 ],当λ=
],当λ=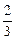 时,S(λ)取得最小值。
时,S(λ)取得最小值。
答:画面高为88 cm,宽为55 cm时,所用纸张面积最小. 如果要求λ∈[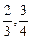 ],当λ=
],当λ=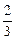 时,所用纸张面积最小。
时,所用纸张面积最小。
则S=(x+16)(λx+10)=λx2+(16λ+10)x+160,
将x=
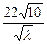 代入上式得
代入上式得 S=5000+44
S=5000+44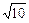 (8
(8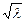 +
+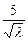 ),
),当8
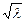 =
=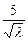 ,即λ=
,即λ=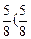 <1)时S取得最小值.
<1)时S取得最小值. 此时高: x=
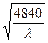 ="88" cm, 宽
="88" cm, 宽 λx=
λx=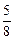 ×88="55" cm.
×88="55" cm.如果λ∈[
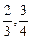 ],可设
],可设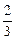 ≤λ1<λ2≤
≤λ1<λ2≤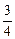 ,
,则由S的表达式得:
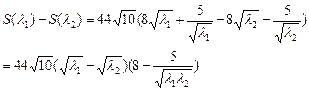
又
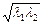 ≥
≥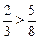 ,故8-
,故8-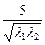 >0,
>0,∴S(λ1)-S(λ2)<0,∴S(λ)在区间[
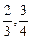 ]内单调递增。
]内单调递增。 从而对于λ∈[
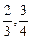 ],当λ=
],当λ=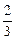 时,S(λ)取得最小值。
时,S(λ)取得最小值。 答:画面高为88 cm,宽为55 cm时,所用纸张面积最小. 如果要求λ∈[
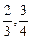 ],当λ=
],当λ=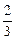 时,所用纸张面积最小。
时,所用纸张面积最小。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
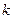 取什么值时,一元二次不等式
取什么值时,一元二次不等式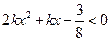 对一切实数
对一切实数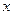 都成立?
都成立?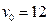 m/s竖直上抛一排球,该排球能够在地面
m/s竖直上抛一排球,该排球能够在地面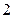 m以上的位置最多停留多长时间?(注:若不计空气阻力,则竖直上抛的物体距离地面的高度
m以上的位置最多停留多长时间?(注:若不计空气阻力,则竖直上抛的物体距离地面的高度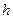 与时间
与时间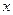 满足关系
满足关系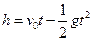 ,其中
,其中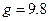 m/s
m/s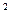 .)
.) ②sin2x+
②sin2x+ ≥4 ③设x,y都是正数,若
≥4 ③设x,y都是正数,若 =1,则x+y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.
=1,则x+y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.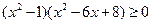
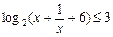 的解集为
的解集为 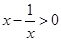 成立的充分不必要条件是
成立的充分不必要条件是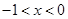 或
或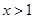 B.
B.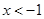 或
或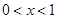 C.
C.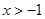 D.
D.