Question

【题目】如图，四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，AC∩BD=O，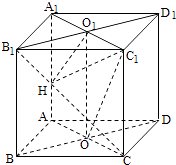
A1C1∩B1D1=O1 ， 四边形ACC1A1和四边形BDD1B1均为矩形．
（1）证明：O1O⊥底面ABCD；
（2）若∠CBA=60°，求二面角C1﹣OB1﹣D的余弦值．

Answer 1

【答案】
（1）证明：∵四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，

∴四边形ABCD为菱形，

又∵AC∩BD=O，

故O为BD的中点，

同理O1也是B1D1的中点，

又∵四边形ACC1A1和四边形BDD1B1均为矩形，

∴O1O∥CC1∥BB1且CC1⊥AC，BB1⊥BD，

∴OO1⊥AC，OO1⊥BD，

又∵AC∩BD=O，AC，BD平面ABCD，

∴O1O⊥底面ABCD；

（2）解：设四棱柱ABCD﹣A1B1C1D1的所有棱长均相等，所以四边形ABCD是菱形，

∴AC⊥BD，

又∵O1O⊥底面ABCD，

∴OB，OC，OO1两两垂直，

如图，以O为坐标原点，OB，OC，OO1所在直线分别为x轴，y轴，z轴建立直角坐标系O﹣xyz．

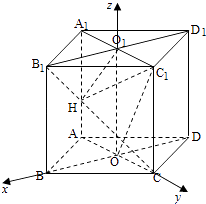
设AB=2，

∵∠CBA=60°，

∴OA=OC=1，OB=OD= ，

则O（0，0，0），B1（ ），C1（0，1，2）

易知， =（0，1，0）是平面BDD1B1的一个法向量，

设 =（x，y，z）是平面OB1C1的一个法向量，则 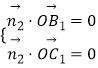，即

取z=﹣ ，则x=2，y=2 ，所以 =（2，2 ，﹣ ）

设二面角C1﹣OB1﹣D的大小为θ，易知θ是锐角，于是：

cosθ=|cos＜ ， ＞|=| |= = ，

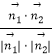故二面角C1﹣OB1﹣D的余弦值为 ．

【解析】（1）由已知中，四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1 ， 四边形ACC1A1和四边形BDD1B1均为矩形．可得O1O∥CC1∥BB1且CC1⊥AC，BB1⊥BD，进而OO1⊥AC，OO1⊥BD，再由线面垂直的判定定理得到O1O⊥底面ABCD；（2）设四棱柱ABCD﹣A1B1C1span>D1的所有棱长均为2a，设AB为2，若∠CBA=60°，OA=OC=1，OB=OD= ，以O为坐标原点，分别以OB，OC，OO1为x，y，z轴正方向建立空间直角坐标系，求出平面BDD1B1和平面OB1C1的法向量，代入向量夹角公式，求出二面角的余弦值．
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．