题目内容
【题目】若函数![]() 有两个极值点
有两个极值点![]() ,其中
,其中![]() ,且
,且![]() ,则方程
,则方程![]() 的实根个数为 .
的实根个数为 .
【答案】5
【解析】
由函数f(x)=﹣lnx+ax2+bx﹣a﹣2b有两个极值点x1,x2,可得2ax2+bx﹣1=0有两个不相等的正根,必有△=b2+8a>0.而方程2a(f(x))2+bf(x)﹣1=0的△1=△>0,可知此方程有两解且f(x)=x1或x2.再分别讨论利用平移变换即可解出方程f(x)=x1或f(x)=x2解的个数.
∵函数f(x)=﹣lnx+ax2+bx﹣a﹣2b有两个极值点x1,x2,
∴f′(x)=﹣![]() +2ax+b=
+2ax+b=![]() ,
,
即为2ax2+bx﹣1=0有两个不相等的正根,
∴△=b2+8a>0.解得x=![]() .
.
∵x1<x2,﹣![]() ,b>0,
,b>0,
∴x1=![]() ,x2=
,x2=![]() .
.
而方程2a(f(x))2+bf(x)﹣1=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2
即有0<x1<x2,:∵x1,x2>0又x1x2=﹣![]() >1
>1
∴x2>1,∵f(1)=﹣b<0∴f(x1)<0,
f(x2)>0.
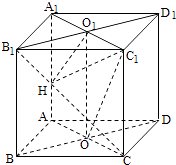
①根据f′(x)画出f(x)的简图,
∵f(x2)=x2,由图象可知方程f(x)=x2有两解,方程f(x)=x1有三解.
综上①②可知:方程f(x)=x1或f(x)=x2共有5个实数解.
即关于x的方程2a(f(x))2+bf(x)﹣1=0的共有5不同实根.
故答案为:5


【题目】教材上一例问题如下:
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
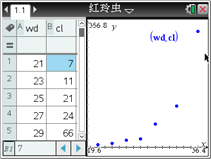
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:
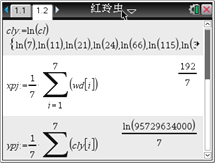
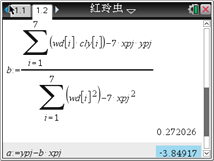
根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)