题目内容
【题目】已知圆
为圆
上任一点.
（1）求
的最大值与最小值；
（2）求
的最大值与最小值.
【答案】（1）最大值是
，最小值是
；（2）最大值是
，最小值是
.
【解析】
（2）试题分析：（1）
是圆上的点与点
连线的斜率，最大、最小值分别是过点
的圆
的两条切线的斜率.设切线的斜率为
，利用圆心到直线的距离等于半径，求出斜率
；（2）令
，则
，转化为线性规划问题求解，平移直线
，当直线和圆
有公共点时，
的范围即可确定，且最值在直线与圆相切时取得.利用点到直线的距离公式，求得
的取值范围.
试题解析：
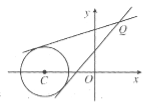
（1）显然可以看作是点与点连线的斜率.令
，如图所示，则其最大、最小值分别是过点
的圆的两条切线的斜率.
对上式整理得
，
∴
，
∴.
故
的最大值是，最小值是.
（3）令，则
可视为一组平行线，当直线和圆有公共点时，的范围即可确定，且最值在直线与圆相切时取得.
依题意，得
，取得
，
故
的最大值是，最小值是.
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】铁矿石A和B的含铁率为
,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
的价格c如下表：
| b(万吨) |
| |
A | 50% | 1 | 3 |
B | 70% | 0．5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元)．
