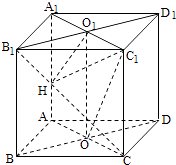
题目内容
【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:
f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
【答案】
(1)解:∵f(t)=10﹣ ![]() =10﹣2sin(
=10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24),
),t∈[0,24),
∴ ![]() ≤
≤ ![]() t+
t+ ![]() <
< ![]() ,故当
,故当 ![]() t+
t+ ![]() =
= ![]() 时,及t=14时,函数取得最大值为10+2=12,
时,及t=14时,函数取得最大值为10+2=12,
当 ![]() t+
t+ ![]() =
= ![]() 时,即t=2时,函数取得最小值为10﹣2=8,
时,即t=2时,函数取得最小值为10﹣2=8,
故实验室这一天的最大温差为12﹣8=4℃.
(2)解:由题意可得,当f(t)>11时,需要降温,由(Ⅰ)可得f(t)=10﹣2sin( ![]() t+
t+ ![]() ),
),
由10﹣2sin( ![]() t+
t+ ![]() )>11,求得sin(
)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,
,
解得10<t<18,即在10时到18时,需要降温.
【解析】(1)利用两角和差的正弦公式化简函数解析式为f(t)10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24),利用正弦函数的定义域和值域求得f(x)的最大值及最小值,可得实验室这一天的最大温差.(2)由题意可得,当f(t)>11时,需要降温,由f(t)>11,求得sin(
),t∈[0,24),利用正弦函数的定义域和值域求得f(x)的最大值及最小值,可得实验室这一天的最大温差.(2)由题意可得,当f(t)>11时,需要降温,由f(t)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,解得t的范围,可得结论.
,解得t的范围,可得结论.
【考点精析】掌握函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

【题目】教材上一例问题如下:
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
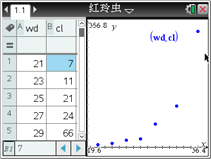
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:
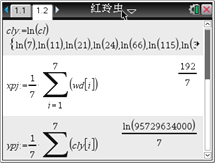
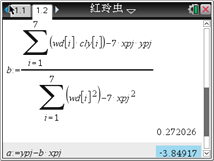
根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)